Question

The three masses shown in (Figure 1) are connected by massless, rigid rods. Assume that m₁ = 180 g and m₂ = 350 g.

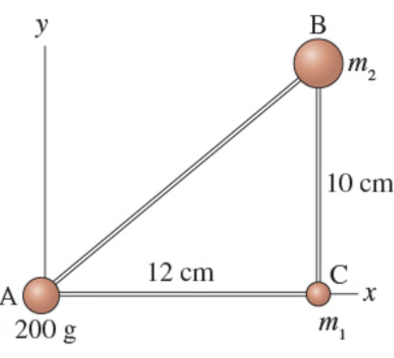
What is the x-coordinate of the center of mass?
Express your answer with the appropriate units.

What is the y-coordinate of the center of mass?
Express your answer with the appropriate units.

Answer 1

Concepts and reason

The main concepts required to solve this problem are the center of mass and distance. Initially, write the equations for the \(x\) and \(y\) -coordinates of the center of mass of the system of three masses. Use this equation and calculate the x-coordinate of the center of mass and y-coordinate of the center of mass of the three masses system.

Fundamentals

Center of mass can be defined as the point in which all the particles of the masses of the system is supposed to be concentrated. The x-coordinate of the center of mass of the system of three masses is, \(x_{C M}=\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}}\)

Here, \(m_{1}\) is the first mass, \(m_{2}\) is the second mass, \(m_{3}\) is the third mass, \(x_{1}, x_{2},\) and \(x_{3}\) are distances of the three masses from the origin respectively in x-axis. The y-coordinate of the center of mass of the system of three masses is, \(y_{C M}=\frac{m 1 y 1+m 2 y 2+m 3 y 3}{m_{1}+m_{2}+m_{3}}\)

Here, \(y_{1}, y_{2}\) and \(y_{3}\) are the vertical distances of the three masses from the origin respectively.

 

(A) The equation for the x-coordinate of the center of mass of the three masses system is, \(x_{C M}=\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}}\)

Substitute \(180 \mathrm{~g}\) for \(m_{1}, 12 \mathrm{~cm}\) for \(x_{1}, 350 \mathrm{~g}\) for \(m_{2}, 12 \mathrm{~cm}\) for \(x_{2}, 200 \mathrm{~g}\) for \(m_{3},\) and 0 for \(x_{3}\) in above equation.

$$ \begin{array}{c} x_{C M}=\frac{(180 \mathrm{~g})(12 \mathrm{~cm})+(350 \mathrm{~g})(12 \mathrm{~cm})+(200 \mathrm{~g})(0)}{(180 \mathrm{~g})+(350 \mathrm{~g})+(200 \mathrm{~g})} \\ =8.71 \mathrm{~cm} \end{array} $$

Part A The x-coordinate of the center of mass of the three masses is \(8.71 \mathrm{~cm} .\)

Explanation \(\mid\) Common mistakes | Hint for next step

Here, the x-coordinate of the center of mass of the three masses is depending on their masses and their distances from the origin in x-axis. The horizontal distance of the mass \(\mathrm{m} 3\) is 0 because the third mass is located at the origin.

 

(B) The equation for the y-coordinate of the center of mass of the three masses is, \(y_{C M}=\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}}{m_{1}+m_{2}+m_{3}}\)

Substitute \(180 \mathrm{~g}\) for \(m_{1}, 0\) for \(y_{1}, 350 \mathrm{~g}\) for \(m_{2}, 10 \mathrm{~cm}\) for \(y_{2}, 200 \mathrm{~g}\) for \(m_{3},\) and 0 for \(y_{3}\) in above equation.

$$ \begin{array}{c} y_{C M}=\frac{(180 \mathrm{~g})(0)+(350 \mathrm{~g})(10 \mathrm{~cm})+(200 \mathrm{~g})(0)}{(180 \mathrm{~g})+(350 \mathrm{~g})+(200 \mathrm{~g})} \\ =4.79 \mathrm{~cm} \end{array} $$

Part B The y-coordinate of the center of mass of the three masses is \(4.79 \mathrm{~cm}\).

Explanation | Common mistakes

Here, the y-coordinate of the center of mass of the three masses is depending on their masses and their distances from the origin in y-axis.

 

Part A

The x-coordinate of the center of mass of the three masses is \(8.71 \mathrm{~cm}\)

Part B

The y-coordinate of the center of mass of the three masses is \(4.79 \mathrm{~cm}\).