Question

Standard Normal Distribution: Assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1.

In each case, draw a graph, then find the probability of the given bone density test scores. both problems below.

a: Less than 1.35

b: Greater than 0.25

will givegreat comments and feedback just need help (:

Answer 1

The test scores are normally distributed with a mean of 0 and a standard deviation of 1

Mean = 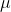= 0

Standard deviation = 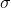= 1

We find the probability of the given bone density test scores

a: Less than 1.35

X = 1.35

We have to find the following probability

--------(1)

We convert above X into z using following formula

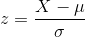---------(2)

Using equation (2) in equation (1)

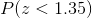
We find above probability using z table of standard normal curve areas

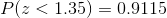
We draw a graph of above probability 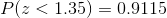are as below

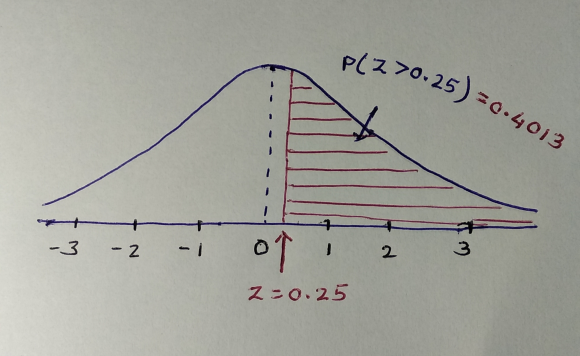
b: Greater than 0.25

X = 0.25

We have to find the following probability

--------(3)

We convert above X into z using following formula

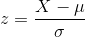---------(4)

Using equation (4) in equation (3)

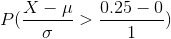
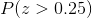
We find above probability using z table of standard normal curve areas

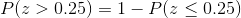
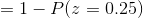
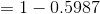
We draw a graph of above probability are as below

Summary :-

a: Less than 1.35 that is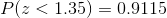  

b: Greater than 0.25  that is