Question

Assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1. Find the probability that a given score is less than -1.82 and draw a sketch of the region.

Assume the readings on thermometers are normally distributed with a mean of 0degrees C and a standard deviation of 1.00degrees C. Find the probability that a randomly selected thermometer reads greater than -1.11 and draw a sketch of the region.

If you could explain how to use the normal distribution table that would be great.

Answer 1

Concepts and reason

Normal distribution: Normal distribution is a continuous distribution of data that has a bell-shaped curve. The \((\mu)\)

normally distributed random variable \(x\) has mean \(^{(\mu)}\) and standard deviation \((\sigma)\). Also, the standard normal distribution represents a normal curve with mean 0 and standard deviation \(1 .\) Thus, the

parameters involved in a normal distribution are mean \((\mu)_{\text {and }}\) standard deviation \((\sigma)\) Standardized z-score: The standardized z-score represents the number of standard deviations the data point is away from the mean.

If the z-score takes a positive value when it is above the mean (0).

If the z-score takes a negative value when it is below the mean (0). 

 

Assumption of Normality:

If the data is large or greater than 30 observations, then it follows the normal distribution with parameter mean \((\mu) \) and standard deviation \((\sigma)\).

 

Fundamentals

Continuous probability distribution: Normal distribution (P was given z) Excel add-in (MegaStat) procedure:

1.In EXCEL, Select Add-Ins > MegaStat > Probability.

2.Choose Continuous probability distributions.

3.Select Normal distribution and select calculate P given z and enter z as

4.Enter mean as \(_{----}\) and standard deviation as \(_{---}\).

5. Click Ok.

 

(1.1) The probability that a given score is less than -1.82 is obtained, as shown below:

From the given information, let the random variable \(X\) be the test scores follows the normal distribution with the population mean as 0 and standard deviation as \(1 .\) The score is less than -1.82.

Instructions to obtain the probability that a given score is less than -1.82 :

1.In EXCEL, Select Add-Ins > MegaStat > Probability.

2.Choose Continuous probability distributions.

3.Select Normal distribution and select calculate P given z and enter z as -1.82.

4.Enter mean as 0 and standard deviation as 1 s.

5.Click Ok.

Follow the above instructions to obtain the following output,

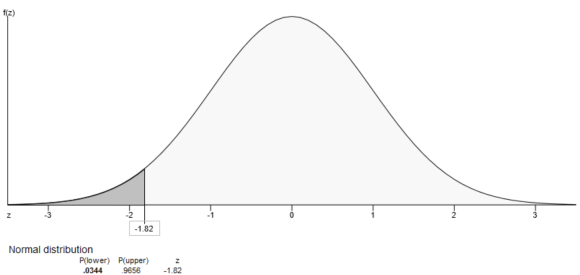
From the output, the probability that a given score is less than -1.82 is 0.0344. That is, \(P(X<-1.82)=0.0344\)

Part 1.1 The probability that a given score is less than -1.82 is \(0.0344 .\)

 

(1.2)

The probability that a given score is less than -1.82 sketch is drawn, as shown below:

Follow the above instructions to obtain the following output,

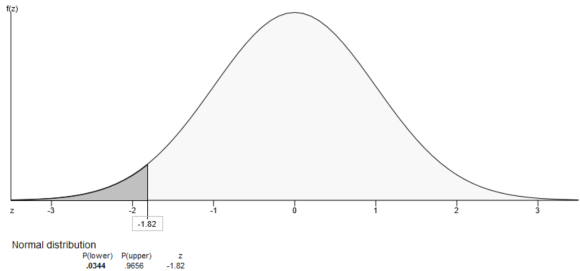
From the output, the probability that a given score is less than -1.82 is 0.0344. That is, \(P(X<-1.82)=0.0344\)

Part 1.2

The probability that a given score is less than –1.82 is 0.0344.

 

(1.3)

The probability that a randomly selected thermometer reads greater than -1.11 is obtained, as shown below:

From the given information, the score is greater than \(-1.11 .\) Instructions to obtain the probability that a randomly selected thermometer reads greater than -1.11:

1.In EXCEL, Select Add-Ins > MegaStat > Probability.

2.Choose Continuous probability distributions.

3.Select Normal distribution and select calculate P given \(z\) and enter \(z\) as \(-1.11 .\)

4.Enter mean as 0 and standard deviation as 1 s.

5. Click Ok.

Follow the above instructions to obtain the following output,

From the output, the probability that a randomly selected thermometer reads greater than -1.11 is \(0.8665 .\) That is, \(P(X>-1.11)=0.8665\)

Part 1.3 The probability that a randomly selected thermometer reads greater than -1.11 is \(0.8665 .\)

 

(1.4) 

The probability that a randomly selected thermometer reads greater than -1.11 sketch is drawn, as shown below:

Follow the above instructions to obtain the following output,

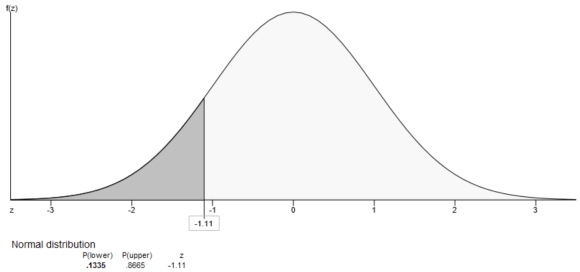
From the output, the probability that a randomly selected thermometer reads greater than -1.11 is 0.8665. That is, \(P(X>-1.11)=0.8665\)

Part 1.4 The probability that a randomly selected thermometer reads greater than -1.11 is \(0.8665 .\)

The probability that a randomly selected thermometer reads greater than –1.11 is obtained by substituting the mean as 0, standard deviation as 1, and score as –1.11 in Excel-MegaStat. There is an 86.65% of chance that a randomly selected thermometer reads greater than –1.11.