Question

1. The following data shows memory scores collected from adults of different ages.

Age (X)	Memory Score (Y)
25	10
32	10
39	9
48	9
56	7

Use the data to find the regression equation for predicting memory scores from age

Group of answer choices

a. Ŷ = 4.33X + 0.11

b. Ŷ = -0.11X + 4.33

c. Ŷ = -0.11X + 13.26

d. Ŷ = -0.09X + 5.4

e. Ŷ = -0.09X + 12.6

1a

Use the regression equation you found in question 21 to find the predicted memory scores for the following age: 28

1b.

Use the regression equation you found in question 21 to find the predicted memory scores for the following age: 43

1c.

Use the regression equation you found in question 21 to find the predicted memory scores for the following age: 50

Answer 1

Solution:

From given data , we prepare a table.

X	Y	XY	X^2	Y^2
25	10	250	625	100
32	10	320	1024	100
39	9	351	1521	81
48	9	432	2304	81
56	7	392	3136	49

n	5
sum(XY)	1745.00
sum(X)	200.00
sum(Y)	45.00
sum(X^2)	8610.00
sum(Y^2)	411.00
Numerator	-275.00
Denominator	302.49
r	-0.9091
r square	0.8265
Xbar(mean)	40.0000
Ybar(mean)	9.0000
SD(X)	11.0454
SD(Y)	1.0954
b	-0.0902
a	12.6066

Now ,

Slope of the regression line is

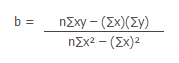
   b =  -0.09

Now , y intercept of the line is

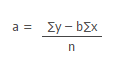
   a =  12.6

The equation of the regression line is

=  bx + a

=  -0.09x + 12.6

Answer : option e =  -0.09x + 12.6

1a) For x = 28 , find the predicted value of y .

Put x = 28 in the regression line equation.

   =  bx + a

= (-0.09*28) + 12.6

Answer:   = 10.08

1b) For x = 43 , find the predicted value of y .

Put x = 43 in the regression line equation.

   =  bx + a

= (-0.09*43) + 12.6

Answer:   = 8.73

1c) For x = 50 , find the predicted value of y .

Put x = 50 in the regression line equation.

   =  bx + a

= (-0.09*50) + 12.6

Answer:   = 8.10