Question

Water Flowing from a Tank

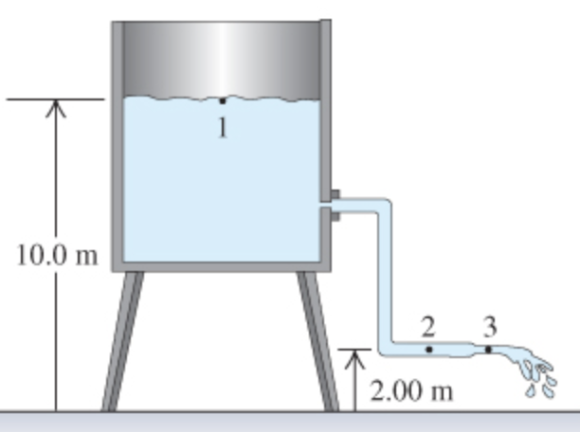
Water flows steadily from an open tank as shown in the figure. (Figure 1) The elevation of point 1 is \(10.0 \mathrm{~m},\) anc the elevation of points 2 and 3 is \(2.00 \mathrm{~m}\). The crosssectional area at point 2 is \(4.80 \times 10^{-2} \mathrm{~m}^{2} ;\) at point 3 where the water is discharged, it is \(1.60 \times 10^{-2} \mathrm{~m}^{2}\). The cross-sectional area of the tank is very large compared with the cross-sectional area of the pipe.

Part A 

Assuming that Bernoulli's equation applies, compute the volume of water \(\Delta V\) that flows across the exit of the pipe in \(1.00 \mathrm{~s}\). In other words, find the discharge rate \(\Delta V / \Delta t\).

Express your answer numerically in cubic meters per second.

\(\frac{\Delta V}{\Delta t}=  \mathrm{~m}^{3} / \mathrm{s}\)

Answer 1

Concepts and reason

The concepts required to solve the given questions is the speed of efflux and the continuity equation. Initially, calculate the discharge area. Later, use the continuity equation. Finally, by using the continuity equation calculate the gauge pressure at point 2 .

Fundamentals

The expression for the speed of efflux is as follows:

\(v=\sqrt{2 g h}\)

Here, \(\mathrm{g}\) is the acceleration due to gravity and \(\mathrm{h}\) is the height. The height of the efflux is as follows:

\(h=y_{1}-y_{2}\)

Here, \(y_{1}\) is the elevation of the point 1 and \(y_{2}\) is the elevation at point 2 . Therefore, the speed of efflux is as follows:

\(v=\sqrt{2 g\left(y_{1}-y_{2}\right)}\)

The expression for the discharge charge is as follows:

\(Q_{3}=v_{3} A_{3}\)

Here, \(v_{3}\) is the speed of efflux and \(A_{3}\) is the area at point \(3,\) where the water is discharged. The expression for the equation of continuity is as follows:

\(A_{2} v_{2}=A_{3} v_{3}\)

Here, \(A_{2}\) is the area at point 2 and \(v_{2}\) is the speed of efflux. The expression to calculate the gauge pressure at point 2 is as follows:

\(P_{2}=\frac{1}{2} \rho\left(v_{3}^{2}-v_{2}^{2}\right)\)

Here, \(\rho\) is the volume charge density.

 

Substitute \(9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}, 10.0 \mathrm{~m}\) for \(y_{1},\) and \(2.00 \mathrm{~m}\) for \(y_{2}\) in the equation \(v=\sqrt{2 g\left(y_{1}-y_{2}\right)}\)

$$ \begin{array}{c} v=\sqrt{2\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)(10.0 \mathrm{~m}-2.00 \mathrm{~m})} \\ =12.52 \mathrm{~m} / \mathrm{s} \end{array} $$

Now, calculate the discharge charge using the equation \(Q_{3}=v_{3} A_{3}\) Substitute \(12.52 \mathrm{~m} / \mathrm{s}\) for \(v_{3}\) and \(0.0160 \mathrm{~m}^{2}\) for \(A_{3}\) in the equation \(Q_{3}=v_{3} A_{3}\)

$$ \begin{array}{c} Q_{3}=(12.52 \mathrm{~m} / \mathrm{s})\left(0.0160 \mathrm{~m}^{2}\right) \\ =0.20 \mathrm{~m}^{3} / \mathrm{s} \end{array} $$

The expression for final velocity is, \(V^{2}-u^{2}=2 g h\)

Substitute 0 for \(u\) in the above equation.

$$ \begin{array}{l} V^{2}=2 g h \\ V=\sqrt{2 g h} \end{array} $$

 

Rearrange the equation \(P_{2}=\frac{1}{2} \rho\left(v_{3}^{2}-v_{2}^{2}\right)\) as follows:

$$ \begin{array}{c} P_{2}=\frac{1}{2} \rho v_{3}^{2}\left(1-\frac{v_{2}^{2}}{v_{3}}\right) \\ =\frac{1}{2} \rho v_{3}^{2}\left(1-\left(\frac{A_{3}}{A_{2}}\right)^{2}\right) \\ =\frac{1}{2} \rho\left(2 g\left(y_{1}-y_{3}\right)\right)\left(1-\left(\frac{A_{3}}{A_{2}}\right)^{2}\right) \\ =\rho\left(g\left(y_{1}-y_{3}\right)\right)\left(1-\left(\frac{A_{3}}{A_{2}}\right)^{2}\right) \end{array} $$

Now, substitute \(1000 \mathrm{~kg} / \mathrm{m}^{3}\) for \(\rho, 9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(\mathrm{g}, 10.0 \mathrm{~m}\) for \(y_{1}, 2.00 \mathrm{~m}\) for \(y_{3}, 0.0160 \mathrm{~m}^{2}\) for \(A_{3}\), and

\(0.0480 \mathrm{~m}^{2}\) for \(A_{2}\) in the equation \(P_{2}=\rho\left(g\left(y_{1}-y_{3}\right)\right)\left(1-\left(\frac{A_{3}}{A_{2}}\right)^{2}\right)\)

$$ \begin{array}{c} P_{2}=\left(1000 \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.8 \mathrm{~m} / \mathrm{s}^{2}(10.0 \mathrm{~m}-2.00 \mathrm{~m})\right)\left(1-\left(\frac{0.0160 \mathrm{~m}^{2}}{0.0480 \mathrm{~m}^{2}}\right)^{2}\right) \\ =\left(1000 \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.8 \mathrm{~m} / \mathrm{s}^{2}(8.00 \mathrm{~m})\right)\left(1-\left(\frac{1}{3}\right)^{2}\right) \\ =6.97 \times 10^{4} \mathrm{~Pa} \end{array} $$

The gauge pressure at point 2 is equal to \(6.97 \times 10^{4} \mathrm{~Pa}\).

The gauge pressure is the amount by which the pressure measured in a fluid exceeds that of the atmosphere, that is, mainly used to measure the pressure difference a system and surrounding atmosphere.

 

The gauge pressure at point 2 is equal to \(6.97 \times 10^{4} \mathrm{~Pa}\).