Question

A study of the ages of motorcyclists killed in crashes involves the random selection of 168 drivers with a mean of 36.53 years. Assuming that σ=8.2 ​years, construct and interpret a 95​% confidence interval estimate of the mean age of all motorcyclists killed in crashes. (Don't round until end of problem)

What is the 95​% confidence interval for the population mean μ​?

______<μ<______

Answer 1

Solution :

Given that,

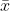= 36.53

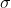= 8.2

n = 168

At 95% confidence level the z is ,

  = 1 - 95% = 1 - 0.95 = 0.05

/ 2 = 0.05 / 2 = 0.025

Z_/2 = Z_0.025 = 1.960

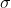
Margin of error = E = Z_/2* (/n)

= 1.960 * (8.2 / 168 )

= 1.24

At 95% confidence interval estimate of the population mean is,

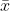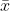- E < < + E

36.53 - 1.24 < < 36.53 + 1.24

35.29 < < 37.77

(35.29 , 37.77)