Question

Formulate the Chinese Remainder Theorem for polynomials over Z/p and prove it. (Please don't just copy and paste another solution onto here)

Answer 1

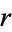Let and 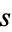be positive integers which are relatively prime and let 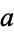and 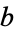be any two integers. Then there is an integer 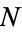such that

N EQ a(mod r) (1)

and

N EQ b(mod s) (2)

Moreover, N is uniquely determined modulo r s.

An equivalent statement is that if 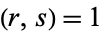, then every pair of residue classes modulo r and s corresponds to a simple residue class modulo .

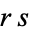The Chinese remainder theorem is implemented in the Wolfram Language as ChineseRemainder[a1, a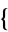2, ...m1, m2, ...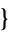]. The Chinese remainder theorem is also implemented indirectly using Reduce in with a domain specification of Integers.

The theorem can also be generalized as follows. Given a set of simultaneous congruences

(3)

for 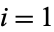, ..., and for which the are pairwise relatively prime, the solution of the set of congruences is

(4)

where

(5)

and the 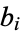are determined from