Question

The dashed lines in the diagram represent cross sections of equipotential surfaces drawn in 1 V increments. (Figure 1)

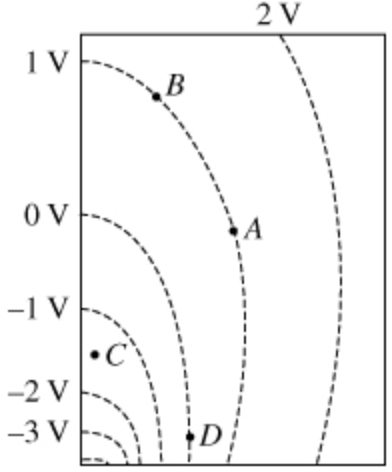
What is the work W_AB done by the electric force to move a 1 C charge from A to B?
Express your answer in joules.

What is the work W_AD done by the electric force to move a 1 C charge from A to D?
Express your answer in joules.

The magnitude of the electric field at point C is

• greater than the magnitude of the electric field at point B.
• less than the magnitude of the electric field at point B.
• equal to the magnitude of the electric field at point B.
• unknown because the value of the electric potential at point C is unknown.

Answer 1

Concepts and reason

The concepts are used to solve this problem is work done by the electric force and electric field. The work done by the electric force to move a charge from one point to another is calculated using the relation between work done and potential energy. The electric field strength can be calculated by using the relation between the electric field strength and the potential energy.

Fundamentals

The surface on which the electric potential is the same at every point is called an equipotential surface. The potential difference between any two points on the equipotential line is equal to zero. The work done \(W\) in moving the charge from one point to the other point is known as the change in electric energy \(-\Delta U\)

\(W=-\Delta U\)

If the work expended by the force is positive, then the potential energy of the object is lowered. Hence, the negative sign is taken for the potential energy change. The change in potential energy is, \(\Delta U=U_{f}-U_{i}\)

Here, \(U_{i}\) and \(U_{f}\) are the initial and final electric potentials. The electric field strength is equal to the negative gradient of the electric potential. The electric potential is defined as the potential energy per unit charge and is given by, \(V=\frac{U}{q}\)

Here, \(\cup\) is the potential energy, and \(\mathrm{q}\) is the charge. The electric field strength is equal to the negative gradient of the electric potential. The change in electric potential between two points is, \(\Delta V=V_{f}-V_{i}\)

Here, \(V_{i}\) and \(V_{f}\) are the electric potentials at initial and final points respectively.

 

The potential difference can be expressed as follows:

\(\Delta V=\frac{\Delta U}{q}\)

Here, q is the charge. Rearrange the above equation for \(\Delta U\). \(\Delta U=q(\Delta V)\)

The change in the electric potential between the points \(A\) and \(B\) is, \(\Delta V=V_{B}-V_{A}\)

Here, \(V_{B}\) is the potential at the point \(B\) and \(V_{A}\) is the potential at the point \(A\). Substitute \(V_{B}-V_{A}\) for \(\Delta V\) in the equation \(\Delta U=q(\Delta V)\) and solve for \(\Delta U\). \(\Delta U=q\left(V_{B}-V_{A}\right)\)

Replace \(\Delta U\) with \(q\left(V_{B}-V_{A}\right)\) in \(W=-\Delta U .\)

\(W=-q\left(V_{B}-V_{A}\right)\)

since the points \(A\) and \(B\) are on the same potential line, they both will have equal amount of electric potential. Substitute \(1 \mathrm{C}\) for \(\mathrm{q}, 1 \mathrm{~V}\) for \(V_{\mathrm{B}},\) and \(1 \mathrm{~V}\) for \(V_{\mathrm{A}}\)

\(W_{A B}=-(1 \mathrm{C})(1 \mathrm{~V}-1 \mathrm{~V})\)

=0

Thus, the work done by electric force to move a 1 C of charge from point A to point \(B\) is \(0 \mathrm{~J}\).

The work is done by the electric force and it is positive. If the work done is positive, then the potential energy of the system decreases. So, the sign of the change in potential energy is negative.

 

Express the work done in moving the charge between the points \(A\) and \(D\) as follows:

\(W_{\mathrm{AD}}=-q\left(V_{\mathrm{D}}-V_{\mathrm{A}}\right)\)

Substitute \(1 \mathrm{C}\) for \(\mathrm{q}, \mathrm{O} \mathrm{V}\) for \(V_{\mathrm{D}},\) and \(1 \mathrm{~V}\) for \(V_{\mathrm{A}}\)

$$ \begin{array}{c} W_{\mathrm{AD}}=-(1 \mathrm{C})(0 \mathrm{~V}-1 \mathrm{~V}) \\ =1 \mathrm{~J} \end{array} $$

Thus, the work done by electric force to move 1 C of charge from point A to point \(D\) is 1 J.

The points \(A\) and \(D\) are on different equipotential surfaces. The point \(D\) is on the equipotential surface on which the electric potential on this surface is \(0 \mathrm{~V}\). The point \(\mathrm{A}\) is on the equipotential surface on which the electric potential is \(1 \mathrm{~V}\).

 

The electric field need not be constant over the equipotential surface. The electric field strength is inversely proportional to the spacing between the equipotential surfaces. The equipotential lines are closer at point \(C\) than the equipotential lines at point \(B\). Hence, the magnitude of the electric field at point \(C\) is not less than or equal to the magnitude of the electric field at point \(B\). The field strength is stronger where the equipotential lines are closer together and weaker where they are farther apart. The equipotential lines are closer at point \(C\) than that at point \(B\). The value of the electric potential at point \(C\) can be calculated and hence it is a known value. The equipotential lines are closer at point \(C\) than the equipotential lines at point \(B\). Hence, the magnitude of the electric field at point \(C\) is greater than the magnitude of the electric field at point \(B\).

Thus, the statement magnitude of the electric field at point \(C\) is greater than the magnitude of the electric field at point \(B\) is correct.

The field strength is stronger where the equipotential lines are closer together and weaker where they are farther apart.