Question

Part A

In the ground-state electron configuration of Fe³⁺, how many unpaired electrons are present?
Express your answer numerically as an integer.

Part B

Build the orbital diagram for the ion most likely formed by phosphorous.
Use the buttons at the top of the tool to add orbital's in order of increasing energy, starting at the bottom with the lowest energy orbitals. Click within an orbital to add electrons.

Answer 1

Concepts and reason

The electrons are filled in the orbitals according to Hund's rule. It states that the pairing of electrons takes place only after all the degenerate orbitals are half-filled. If an atom loses electrons, it gets a positive charge, and if the atom gains electrons, it gets a negative charge.

Fundamentals

The ground state is the molecule's energy state when all the electrons are present in the lowest possible molecular orbitals. In an excited state, one electron goes from lower energy orbital to higher energy molecular orbital.

 

\(\mathbf{A}\)

The atomic number of Fe is 26.

It loses 3 electrons to form \(\mathrm{Fe}^{3+}\) ion.

Hence, the number of electrons in \(\mathrm{Fe}^{3+}\) is 23 . Therefore, its ground state electron configuration is,

\(1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{5}\)

Write the orbital configuration for the outermost \(3 \mathrm{~d}\) orbital as follows:

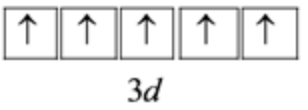
Hence, the number of unpaired electrons in \(\mathrm{Fe}^{3+}\) are 5 .

In the \(3 \mathrm{~d}\) subshell, there are 5 degenerate \(\mathrm{d}\) orbitals. Hence, according to Hund's rule, each orbital gets one electron and a total of 5 unpaired electrons.

 

\(\mathbf{B}\)

The most likely ion formed by phosphorous is \(\mathrm{P}^{3-}\).

The electron configuration of \(\mathrm{P}^{3-}\) is,

\(1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6}\)

The orbital diagram for \(\mathrm{P}^{3-}\) is as follows:

The atomic number of phosphorous is 15. Its electron configuration is,

\(1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{3}\)

It needs 3 electrons to attain an inert gas configuration.

Hence, the most likely ion formed by phosphorous is \(\mathrm{P}^{3-}\).