Question
In: Statistics and Probability
14 randomly chosen students have each won a free ticket to play a game of chance....
14 randomly chosen students have each won a free ticket to play a game of chance. In this game a wheel is spun that has been equally divided among 20 values, and when the wheel stops spinning a pointer will have selected one of the 20 values randomly (think Wheel-of-Fortune style). So therefore we will assume that each of the 20 outcomes is equally likely. Before spinning, the player chooses which value they think it will stop on. If it stops on the value chosen, they win $300. If it stops on the position to the left or right of the value chosen, they still win $100 for getting close. Otherwise, they win nothing. What is the probability that exactly 3 of the students will win some money? Leave your answer as a decimal.
Solutions
Expert Solution
Number of students randomly chosen to play a game of chance = 14
Number of values equally divided on the wheel = 20
Total number of outcomes =20
Player will win some money, if it stops on the value chosen or if it stops on the position to the left or right or the value chosen.
Number of outcomes that favor the Player will win some money= 3
p: Probability that a player will some money
= Number of outcomes that favor the Player will win some money/ Total number of outcomes = 3/20=0.15
X : Number of the students will win some money
X follows Binomial distribution with n= 14 and p =0.15
Probability mass function of X is given by :
Probability that 'r' students will win some money = P(X=r)
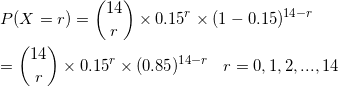
 probability
that exactly 3 of the students will win some money = P(X=3)
probability
that exactly 3 of the students will win some money = P(X=3)
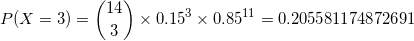
 probability
that exactly 3 of the students will win some money =
0.205581174872691
probability
that exactly 3 of the students will win some money =
0.205581174872691
Related Solutions
12) You have a 14% chance of winning when you play a certain game. You play...
A game of chance offers the following odds and payoffs. Each play of the game costs...
Problem 12. Peter and Paula play a game of chance that consists of several rounds. Each...
Suppose we have a 20% chance of winning a game and play 30 times. What is...
A lottery game is played in many places and requires $1 per ticket to play. To...
Ann and Bill play the following game in which 4 gold coins are to be won....
Consider a gambling game where a player pays $10 to play with a 40% chance of...
Diane has decided to play the following game of chance. She places a $1 bet on...
street performer offers you a chance to play his game for the low price of $10....
P 2-10: Verdi Opera or Madonna? You won a free ticket to see Verdi's Aida opera....
- My industry is Optometry: 7. What are the impacts of the macroeconomic business cycle on demand...
- Compute Bond Proceeds, Amortizing Discount by Interest Method, and Interest Expense Boyd Co. produces and sells...
- Which of the following is a typical characteristic of human traits that follow an X-linked recessive...
- Finding Z scores for a Standard Normal Distribution 1.) Find the z score that has an...
- Drug money extract in the 5.0 mL methanol containing cocaine gave a signal of 4.27 mV...
- (a) Suppose you are given the following (x, y) data pairs. x: 1 2 6 y:...
- Many people have different concepts or ideas about the study of economics. It would be interesting...
 orchestra answered 3 years ago
orchestra answered 3 years ago