Question

In: Math

Administrative assistants in a local university have been asked to prove their proficiency in the use...

Administrative assistants in a local university have been asked to prove their proficiency in the use of spreadsheet software by taking a proficiency test. Historically, the mean test score has been 74 with a standard deviation of 4. A random sample of size 40 is taken from the 100 administrative assistants and asked to complete the proficiency test.

What is the probability that the sample mean score is more than 75, the predetermined passing score?

Expert Solution

Solution :

Given that ,

mean = = 74

standard deviation = = 4

n = 40

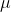
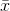= = 74

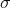
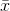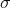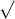= / n = 4 / 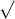40 = 0.632

P( > 75) = 1 - P(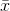 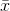< 75)

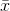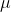
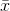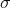
= 1 - P[( - ) / 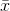< (75 - 74) / 0.632]

= 1 - P(z < 1.58)

Using z table,

= 1 - 0.9429

= 0.0571

milcah answered 16 hours ago

As the representative of the local accounting club, you have been asked by the dean to...

As the representative of the local accounting club, you have been asked by the dean to help her understand the costs of the different degrees offered at the school. You decide to use an activity-based cost system. Write a report outlining the first two steps of developing an ABC system for this purpose: (1) Identify the activities, and (2) identify the activities associated with each activity.

You have been asked by a Finance Club at a University to enter an essay competition...

You have been asked by a Finance Club at a University to enter an essay competition that should evaluate and examine the existing laws and regulations that governs commercial banking activities in your current jurisdiction. . For the essay competition they have outlined the following key points of focus: • Outline and discuss three reasons why it is necessary to regulate banks. • Provide and evaluate three reasons why some banks have failed within your jurisdiction. Instructions: Essay should be...

You have been asked to serve as a consultant for a local support group for cancer...

You have been asked to serve as a consultant for a local support group for cancer patients. They would like you to do the following: 1) provide a presentation on health literacy; 2) draft a handout on how to find quality information related to cancer care, study findings, and treatment implications based upon study findings. As you prepare for both of these charges, what would be some key points and resources that you would want to share with the group?

You have been asked by the board of trustees of a local church to review its...

You have been asked by the board of trustees of a local church to review its accounting procedures. As part of this review you have prepared the following comments relating to the collections made at weekly services and record keeping for members’ pledges and contributions: The church’s board of trustees has delegated responsibility for financial management and the financial records to the finance committee. This group prepares the annual forecast and approves major disbursements, but is not involved in collections...

You are a medical assistant at a local hospital. You have been asked to give a...

You are a medical assistant at a local hospital. You have been asked to give a presentation on the diagnosis and treatment of latent tuberculosis infection. The presentation will be open to the public so instead of presenting a real patient case, you decide to create a fictional sample case. Create a single case and list the characteristics of the person you will be testing and treating. Describe basic information about the patient including age, sex, lifestyle, and pertinent medical...

For this task, assume that you have been asked to host a local forum for parents...

For this task, assume that you have been asked to host a local forum for parents of junior high school aged children to discuss the consequences of having sex at an early age. Parents are debating the following topic: A sexuality education unit, at least a week in length, should be included in all grades in all schools. After the debate you are to draft a summary of the conversations. In your paper, provide both the pro and con of...

7. Employees of a local university have been classified according to gender and job type as...

7. Employees of a local university have been classified according to gender and job type as shown below. Job Male (M) Female (F) Faculty (FA) 110 10 Salaried staff (SS) 30 50 Hourly staff (HS) 60 40 (A) If an employee is selected at random what is the probability that the employee is male? (B) If an employee is selected at random what is the probability that the employee is male and salaried staff? (C) If an employee is selected...

Conduct a research design. You have been asked by a university to determine whether living in...

Conduct a research design. You have been asked by a university to determine whether living in dormitories improves student satisfaction and learning outcomes. Propose a research design to assess this question. Good answers will invoke parts of the research design process that we have been discussing: research questions; hypotheses; dependent variable; independent variable; population targeted; unit of analysis; data collection strategy; plan of analysis (i.e., what will you be comparing?).

You have been asked to make a short presentation to the manager of your local community...

You have been asked to make a short presentation to the manager of your local community mental health centre about the value in adopting a MedTEAM or an Illness Management and Recovery (IMR) approach to working with people with psychiatric disabilities. Pick ONE aspect of MedTEAM or IMR that you'd like to promote. state: how that aspect will benefit client outcomes and at least one point of evidence (with reference) supporting your claim. also discuss the psychiatric rehabilitation guiding principle/s...

You have been asked by the board of the local hockey club to review its accounting...

You have been asked by the board of the local hockey club to review its accounting procedures. You have made the following observations in regards to cash collected for annual dues and for weekly entrance ticket sales. The club's board has given financial management and audit of the financial records responsibility to the finance committee. This team prepares the budget and approves all major cash disbursements. No audit has been considered necessary in recent years because the same trusted employee...