Question

A charged nonconducting rod, with a length of 3.68 m and a cross-sectional area of 2.79 cm2, lies along the positive side of an x axis with one end at the origin. The volume charge density ρ is charge per unit volume in coulombs per cubic meter. How many excess electrons are on the rod if ρ is (a) uniform, with a value of -2.07 µC/m3, and (b) nonuniform, with a value given by ρ = bx2, where b = -2.89 µC/m5?

Answer 1

Here,
Length of  charged nonconducting rod L= 3.68m
cross-sectional area  A=2.79cm² or
Volume charge density is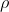

(a) If the charge density on rod is uniform:

Charge on rod is given by    {V is volume of the rod}
or     {A is area and L is length}
  
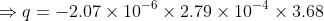
C

  Excess of electron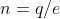
  
  
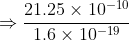
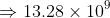
So, This is the number of excess of electron on the rod, Negative sign was neglected because that show only the nature of charge.

(b) Charge density is non uniform on the rod:
Now the charge for any specific point where the charge density is 2B(because it is not at every point)
So charge on whole rod is given by-

Because charge density is non uniform so let it covers x portion of the rod

  
  


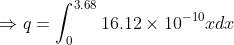
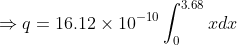
Excess of electron: n=q/e