Question

A 95% confidence interval for the average waiting time at the drive-thru of a fast food restaurant if a sample of 192 customers have an average waiting time of 92 seconds with a population deviation of 23 seconds

round to the nearest hundredth of a second

Answer 1

Solution :

Given that,

Point estimate = sample mean = = 92

Population standard deviation =    = 23

Sample size = n =192

At 95% confidence level the z is ,

= 1 - 95% = 1 - 0.95 = 0.05

/ 2 = 0.05 / 2 = 0.025

Z_/2 = Z _0.025 = 1.96   ( Using z table ( see the 0.025 value in standard normal (z) table corresponding z value is 1.96 )

Margin of error = E = Z/2 * ( 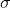/n)

= 1.96* ( 23/   192)

E= 3.25
At 95% confidence interval estimate of the population mean
is,

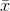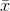- E < < + E

92- 3.25 <   <92 + 3.25

88.75 <   < 95.25
(88.75 , 95.25)

At 95% confidence interval estimate of the population mean is ( 88.75 second and  95.25  second )