Question

**Convert all units to MKS**

1. In some collisions, KE is less after the collision than before. Since energy

cannot be lost, what happened to it? What could you do to show this is true?

2. A 2.00g bullet strikes a 2.00kg block hanging from a long cord. The bullet imbeds itself in the block causing the block with bullet embedded to swing upwards to a height of 50.0 cm above its original position.

A. What type of collision best describes the bullet striking the block?

B. Do a walk-through of the energy of the system starting just before the bullet strikes the block and continue until the block and bullet reach max height.

C. Find the velocity of the bullet before it collides with the block.

3. A 450g rubber ball is dropped from 2.0m above the floor. After the bounce, the ball only rises to a height of 1.5m above the floor.

A. Determine the change in momentum of the ball when it hits the floor and bounces up. (hint: either use motion equations or conservation of energy to determine the speed of the ball when it reaches the floor.)

B. Calculate the amount of heat generated when the ball hits the floor.

C. Explain how momentum is conserved when the ball collides with the floor.

Answer 1

1 Some of the kinetic energy will be converted to heat energy and sound energy and some energy may be used in deforming the two or more objects that collided and that would result in lessened kinetic energy

I have solved this question earlier with different figures. Please workout using yours figures. If you need any further help just PM me. If I have helped you please rate me 5 stars first (before you rate anyone else).

2 A 2.00g bullet strikes a 2.00kg block hanging from a long cord. The bullet imbeds itself in the block causing the block to swing upwards to a height of 75cm above its original position. A. What type of collision best describes the bullet striking the block? B. Do a walk-through of the energy of the system starting just before the bullet strikes the block. C. Find the velocity of the bullet before it collides with the block.

KE at start = 1/2(M+m)V^2

energy at end is all potential = (M+m)gh where h is the height of the block above the surface and is equal to
L-Lcos(theta) = L(1-cos(theta))

so, we equate PE and KE:

(M+m)gL(1-cos(theta))=1/2(M+m)V^2

the factors of M+m cancel; since we know g, L and theta, we can solve for V (speed after collision)

we now go back to the original momentum equation:

mv=(M+m)V and solve for v=(M+m)V/m

3 A 450g rubber ball is dropped from 2.0m above the floor. After the bounce, the ball only rises to a height of 1.5m above the floor.

A. Determine the change in momentum of the ball when it hits the floor and bounces up.



B. Calculate the amount of heat generated when the ball hits the floor.



C. Explain how momentum is conserved when the ball collides with the floor.
(hint: either use motion equations or conservation of energy to determine the speed of the ball when it reaches the floor.)

A) Using energy:

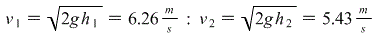
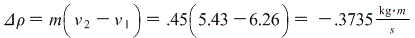
b) the heat is the amount of energy lost:

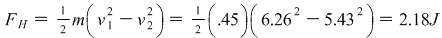
C) see above for conservation of energy. Initial KE = Final KE + Heat