Question

The following objects are released simultaneously from rest at the top of a 1.35m long ramp inclined at 3.10 degrees to the horizontal: a solid sphere, a solid cylinder, a hollow cylindrical shell, and a hollow ball.

Which wins the race? The solid Sphere won, I just cant get the positions of the other 3 objects

At the moment the winner reaches the bottom, find the positions of the other three objects.

please explain....

Answer 1

We have the equation for an inclined plane for velocity and acceleration as

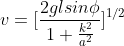
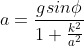
solid sphere

k²/a²=2/5=0.4

Thus we have v=[2*9.8*1.35*sin[3.10^o ]/1.4]^1/2 = 0.87 m/s

a=[9.8*sin[3.10^o ]/1.4]=0.38 m/s²

Solid cylinder

k²/a²=1/2=0.5

Thus we have v=[2*9.8*1.35*sin[3.10^o ]/1.5]^1/2 = 0.98 m/s

a=[9.8*sin[3.10^o ]/1.5]=0.35 m/s²

Hollow cylindrical shell

k²/a²=1

Thus we have v=[2*9.8*1.35*sin[3.10^o ]/2]^1/2 = 0.85 m/s

a=[9.8*sin[3.10^o ]/1]=0.53 m/s²

Hollow ball   [case of hollow sphere]

k²/a²=2/3=0.67

Thus we have v=[2*9.8*1.35*sin[3.10^o ]/1.67]^1/2 = 0.93 m/s

a=[9.8*sin[3.10^o ]/1.67]=0.32 m/s²

Object having the maximum speed wins the race.Hence Solid cylinder wins the race.

Position of solid sphere

Using the kinematic equation,v²= u²+2as   [u=0m/s]

s= v²/2a=0.87²/2*0.38= 0.99m

Position of solid cylinder

Using the kinematic equation,v²= u²+2as   [u=0m/s]

s= v²/2a=0.98²/2*0.35= 1.37m

Position of Hollow cylinder shell

Using the kinematic equation,v²= u²+2as   [u=0m/s]

s= v²/2a=0.85²/2*0.53= 0.68m

Position of Hollow ball

Using the kinematic equation,v²= u²+2as   [u=0m/s]

s= v²/2a=0.93²/2*0.32= 1.35m