Question
In: Statistics and Probability
Discuss in not more than 100 words the purposes of hypothesis testing in quantitative research. Illustrate...
Discuss in not more than 100 words the purposes of hypothesis testing in quantitative research. Illustrate your answers with at least one example in the construction industry.
Solutions
Expert Solution
A null hypothesis is a hypothesis that says there is no statistical significance between the two variables. It is usually the hypothesis a researcher or experimenter will try to disprove or discredit. An alternative hypothesis is one that states there is a statistically significant relationship between two variables
Hypothesis Testing for Small Sample Quantitative Data
Learning Objective:
-
Learn how to conduct a hypothesis test with a small number of observations for quantitative data.
Hypothesis Test
Step 1: Make assumptions about your data
- For these tests, we assume that our data is quantitative and that the population is normally distributed. We also know that our sample size is going to be relatively small, which means that we will be referencing the t table rather than the z table.
Step 2: Formulate null and alternative hypotheses
- Just like with other types of hypothesis testing, the null is what a determined skeptic would believe about what we are going to measure, and the alternative hypothesis is our research hypothesis based on the data collected.
- As with other types of hypothesis testing, this test can be either one-sided or two-sided. Make sure you keep in mind how you intend to test the data.
Step 3: Calculate a Test Statistic
- This statistic summarizes how much our alternative hypothesis differs from the rest of the data if the null was true. Here is the formula, which we’ve used many times before:
- Test statistic = ( Xbar -
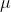 )/(s/sqrt(n))
)/(s/sqrt(n)) - Don’t forget to note the degrees of freedom!
- d.f.= n-1
Step 4: Calculate a p-value
- Remember, a p-value is a measure of surprise, so small p-values more strongly contradict the null because that means it would be extremely surprising to see the results of our alternative hypothesis if the null were true.
- To find the p-value, go to this t table or we can use R.
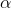 Keep in mind the confidence interval, the degrees of freedom, and
if the hypothesis is one or two-sided.
Keep in mind the confidence interval, the degrees of freedom, and
if the hypothesis is one or two-sided.
Step 5: Draw a conclusion
- Are the results statistically significant given the
pre-determined
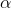 level
level - If p value <
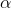 we reject the null and conclude that the evidence supports the
alternative hypothesis. If p- value >
we reject the null and conclude that the evidence supports the
alternative hypothesis. If p- value > 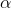 .we fail to reject the null.
.we fail to reject the null.
Related Solutions
Can you provide an example of hypothesis testing in quantitative research and one in qualitative research?
State the difference between qualitative and quantitative data. not more than 200 words
Discuss the common uses and applications of three or more sample hypothesis testing.
In more than 100 words, describe the nature and characteristics of corporations.
Hypothesis Testing: Claim: Females are more likely than males to wear masks at the grocery store....
In not more than thousand (100) words write an essay on the topic “ the impact...
Discuss sources of bias for both quantitative and qualitative research. For quantitative research, be sure to...
Management Accounting: It’s more than just crunching numbers. Discuss. (more than 500 words)
Write this in your own words, using no more than 100 words: Express how the durability...
In your own words, describe what you have learned about hypothesis testing and hypothesis testing for...
- (a) Suppose you are given the following (x, y) data pairs. x: 1 2 6 y:...
- Many people have different concepts or ideas about the study of economics. It would be interesting...
- 2.70 moles of an ideal gas with CV,m=5R/2are transformed from an initial state T = 660....
- A 10 g bullet traveling at 430m/s str
- Suppose the Madison city government imposes a price ceiling on the rental price of apartments.The demand...
- Magnolia Manufacturing makes wing components for large aircraft. Kevin Choi is the production manager, responsible for...
- distinguish between microeconomics and macroeconomics
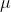 )/(s/sqrt(n))
)/(s/sqrt(n))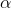 Keep in mind the confidence interval, the degrees of freedom, and
if the hypothesis is one or two-sided.
Keep in mind the confidence interval, the degrees of freedom, and
if the hypothesis is one or two-sided. orchestra answered 3 years ago
orchestra answered 3 years ago