Question

a. Briefly describe what a commutator is using words and an equation. How do commutators relate to the uncertainty principle?

b. Use the angular momentum commutators to show why we can not simultaneously determine the z-component of angular momentum and the x and/or y components.

Answer 1

a) In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theoryand ring theory.

he commutator of two elements, g and h, of a group G, is the element

[g, h] = g⁻¹h⁻¹gh.

It is equal to the group's identity if and only if g and h commute (i.e., if and only if gh = hg). The subgroup of G generated by all commutators is called the derived group or thecommutator subgroup of G. Note that one must consider the subgroup generated by the set of commutators because in general the set of commutators is not closed under the group operation. Commutators are used to define nilpotent and solvable groups.

The above definition of the commutator is used by some group theorists, as well as throughout this article. However, many other group theorists define the commutator as

[g, h] = ghg⁻¹h⁻¹

As we discussed in the Linear Algebra lecture, if two physical variables correspond to commuting Hermitian operators, they can be diagonalized simultaneously—that is, they have a common set of eigenstates. In these eigenstates both variables have precise values at the same time, there is no “Uncertainty  Principle” requiring that as we know one of them more accurately, we increasingly lose track of the other.  For example, the energy and momentum of a free particle can both be specified exactly.  More interesting examples will appear in the sections on angular momentum and spin.

But if two operators do not commute, in general one cannot specify both values precisely.  Of course, such operators could still have some common eigenvectors, but the interesting case arises in attempting to measure A and B simultaneously for a state in which the commutator has a nonzero expectation value, .

A Quantitative Measure of “Uncertainty”

Our task here is to give a quantitative analysis of how accurately noncommuting variables can be measured together. We found earlier using a semi-quantitative argument that for a free particle, at best.  To improve on that result, we need to be precise about the uncertainty in a state

We define as the root mean square deviation:

To make the equations more compact, we define by

(We’ll put a caret (a hat) on the to remind ourselves it’s an operator—and, of course, it’s a Hermitian operator, like A.)   We also drop the bra and ket, on the understanding that this whole argument is for a particular state. Now

Introduce an operator B in exactly similar fashion, having the property that .

2)

In general, in quantum mechanics, when two observable operators do not commute, they are called complementary observables. Two complementary observables cannot be measured simultaneously; instead they satisfy an uncertainty principle. The more accurately one observable is known, the less accurately the other one can be known. Just as there is an uncertainty principle relating position and momentum, there are uncertainty principles for angular momentum.

The Robertson–Schrödinger relation gives the following uncertainty principle:

where 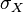is the standard deviation in the measured values of X and denotes the expectation value of X. This inequality is also true if x,y,z are rearranged, or if L is replaced by J or S.

Therefore, two orthogonal components of angular momentum (for example L_x and L_y) are complementary and cannot be simultaneously known or measured, except in special cases such as .

It is, however, possible to simultaneously measure or specify L² and any one component of L; for example, L² and L_z. This is often useful, and the values are characterized by theazimuthal quantum number (l) and the magnetic quantum number (m). In this case the quantum state of the system is a simultaneous eigenstate of the operators L² and L_z, butnot of L_x or L_y. So, we can not simultaneously determine the z-component of angular momentum and the x and/or y components.