Question

Return on a risk-free investment is 3 percent and the expected market return is 6 percent. Annualized stdev of the return on the market is 15 percent.

Project 1: IRR = 7 percent. SD(ri) = .45 Corr (Ri, Rm) = .25

Project 2: IRR = 11 percent. SD(ri) = .30 Corr (Ri, Rm) = .90

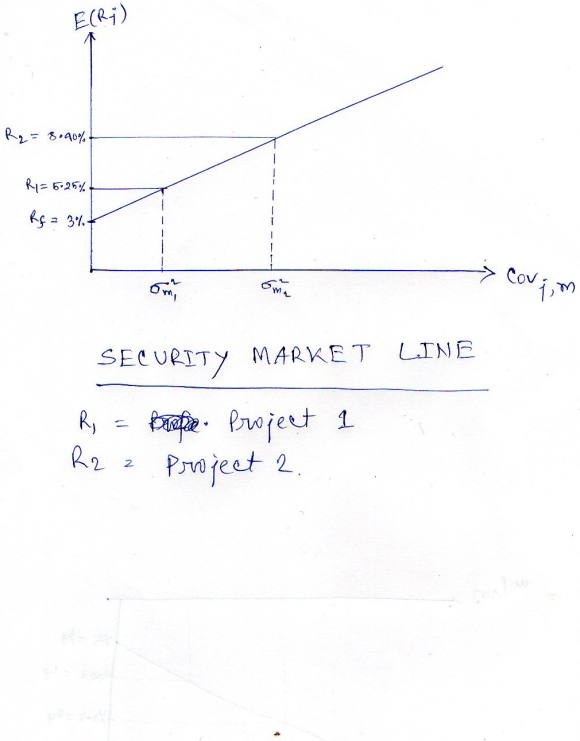
Please find and graph the security market line

Please find the index of systematic risk of each project and plot the IRR combinations on a graph and rank the projects according to a measure of their total risk and then their index of systematic risk.

Answer 1

SML(Security Market Line) Equation:-

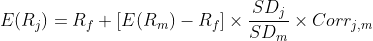
Here, E(Rj) = Expected Portfolio Return

Rf = Risk-Free Return = 0.03

E(Rm) = Expected Market Return = 0.06

SDj = Standard Deviation of Return = SD(ri)

SDm = Standard Deviation of Market Return = SD(m) = 0.15

For Project 1:-

E(Rj) = 0.03 + [0.06 - 0.03] * (0.45 / 0.15) * 0.25 = 0.03 + 0.03 * 3 * 0.25 = 0.0525

So, Portfolio Return = 5.25 %

For Project 2:-

E(Rj) = 0.03 + [0.06 - 0.03] * (0.30 / 0.15) * 0.90 = 0.03 + 0.03 * 2 * 0.9 = 0.084

So, Portfolio Return = 8.40 %

We can get the systematic risk from the value of "Beta".

If Beta is greater than 1, that means the project is riskier than the market portfolio. We can also use Beta as to compare risk of two projects. Whichever has a higher Beta, has high Risk.

Systematic Risk of Project 1,

  

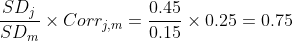
Systematic Risk of Project 2,

So, here we can say that Project 2 is more Riskier.