Vector-Valued Functions

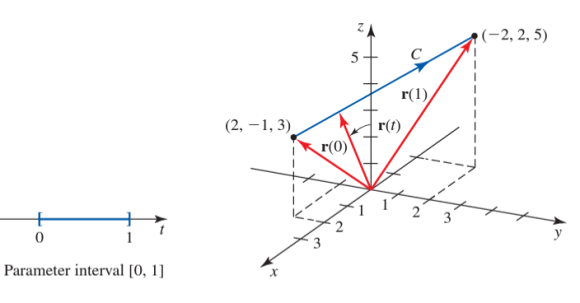
Exercise. Sketch the curve defined by the vector function

r( t ) = ( 2 - 4t )i + ( −1 + 3t )j + ( 3 + 2t )k , where 0≤t≤1

Expert Solution

Solution

The parametric equations for the curve are

x = 2 - 4t , y = -1 + 3t , z = 3 + 2t

which are parametric equations of the line passing through the point

( 2 , -1 , 3 ) with direction numbers -4 , 3 , and 2. Because the parameter interval is the closed interval [ 0 , 1 ] , we see that the curve is a straight line segment : Its initial point ( 2 , -1 , 3 ) is the terminal point of the vector

r(0)2i-j +3k , and its terminal point ( -2 , 2 , 5 ) is the terminal point of the vector r(1) = -2i + 2j + 5k . ( See Figure 4. )

SUN BUNRA answered 2 years ago

Which of the following are subspaces of the vector space of real-valued functions of a real...

Which of the following are subspaces of the vector space of real-valued functions of a real variables? (must select all of the subspaces.) A. The set of even function (f(-x) = f(x) for all numbers x). B. The set of odd functions (f(-x) = -f(x) for all real numbers x). C. The set of functions f such that f(0) = 7 D. The set of functions f such that f(7) = 0

1.29 Prove or disprove that this is a vector space: the real-valued functions f of one...

1.29 Prove or disprove that this is a vector space: the real-valued functions f of one real variable such that f(7) = 0.

Consider the vector functions ?(?) and ?(?), where ?(?) = 〈? sin ? , ? cos...

Consider the vector functions ?(?) and ?(?), where ?(?) = 〈? sin ? , ? cos ? , ?^2〉, ?(?) = 〈1, −1, 1〉, and ?′(?) = 〈1, 0, −1〉. Define ?(?) = ?(?) × ?(?) and find ?′(?)

For the following 2 functions, find a unit vector at the specified point for the following...

For the following 2 functions, find a unit vector at the specified point for the following function, allowing the function to increase the fastest in this direction, and find the fastest rate of change. 1) f(x,y) = e^x(siny) , P(0, 3/π) 2) f(x,y,z) = arctan (x+y+z), P(1,1,1)

verify the assertion. (Subspace example) 1) The set of continuous real-valued functions on the interval [0,1]...

verify the assertion. (Subspace example) 1) The set of continuous real-valued functions on the interval [0,1] is a subspace of R^[0,1] This is from Linear Algebra Done Right- Sheldon Axler 3rd edition. I don't understand why the solution uses a integral.

Question 3. Determine if the following vector fields are conservative. If they are,find their potential functions....

Question 3. Determine if the following vector fields are conservative. If they are,find their potential functions. a.F=〈y,x+z,−y〉. b.F=〈y+z,x+z,x+y〉.

Let V be the vector space of all functions f : R → R. Consider the...

Let V be the vector space of all functions f : R → R. Consider the subspace W spanned by {sin(x), cos(x), e^x , e^−x}. The function T : W → W given by taking the derivative is a linear transformation a) B = {sin(x), cos(x), e^x , e^−x} is a basis for W. Find the matrix for T relative to B. b)Find all the eigenvalues of the matrix you found in the previous part and describe their eigenvectors. (One...

1. Writing new functions for the following: Find the magnitude of a vector (as one function...

1. Writing new functions for the following: Find the magnitude of a vector (as one function that works on both 2D and 3D vectors). Normalize a vector (also working for both 2D and 3D). Compute the dot product of two vectors. Compute the cross product of two vectors. Get the distance between two positions. Get the angle between two vectors. Get a point on a ray (given the origin, direction, and parametric value along ray). 2. Use Python lists to...

Let C(R) be the vector space of continuous functions from R to R with the usual...

Let C(R) be the vector space of continuous functions from R to R with the usual addition and scalar multiplication. Determine if W is a subspace of C(R). Show algebraically and explain your answers thoroughly. a. W = C^n(R) = { f ∈ C(R) | f has a continuous nth derivative} b. W = {f ∈ C^2(R) | f''(x) + f(x) = 0} c. W = {f ∈ C(R) | f(-x) = f(x)}.

Formulate the definitions of linear dependence and independence of a set of k vector functions f1(x),...

Formulate the definitions of linear dependence and independence of a set of k vector functions f1(x), ... , fk(x) continuous on an interval I.

Question