Question

Consider the regression we know that f there is a strong linear correlation between X and Z, then it is more likely that the t-test statistics get smaller. Show and explain how. Explain what happens if t-statistics get smaller.

Answer 1

1. If there is a strong correlation between X and Z, then Cov(x,z)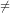0

The t statistic is given by :

t = , where is the hypothesised value

and ,

s.e(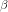) = and variance is

var() =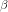

where R_k² is the coefficient of determination of auxiliary regression of x_k on other regressors.

• When X and Z are uncorrelated, R_k²=0 and var()=
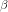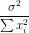
• When X and Z are correlated, then R_k²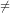0

Then , since R² is less than or equal to 1, the denominator decreases (since now it is multiplied by a number less than 1) and hence the variance and consequently the standard error of coefficient increases.

Due to increase in standard error, the denominator in t statistic, i.e

t = will increase and hence the t statistics becomes smaller.

Hence, due to strong linear correlation between X and Z, the standard error increases and hence the denominator of t statistics increase result in a smaller t statistic.

2. When the t statistics gets smaller, our standard errors increase while the confidence intervals become wider.

Let,

H₀: 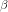=0

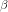
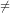H1: 0

We reject the null hypothesis based on t test when: t > t_critical

Due to presence of correlation between regressors, t statistics become smaller and hence probability of rejecting the null hypothesis will reduce ( also due to increase in confidence intervals which are acceptance regions). It is likely that we will accept the null hypothesis and the coefficient will come out to be statistically insignificant.

This is the problem of multicollinearity caused by correlation between regressors which results in few significant t ratios.