Question

I. What is the difference between a standing wave in a string and a wave that progresses within a string?

a) in a standing wave the location of maximums and minimums along the string is constant in time.

b) in a wave that progresses the velocity of the wave changes with time.

c) in a standing wave the wavelength is constant, whereas in a progressing wave it is not

d) a standing wave is only created by having an external motor moving the string in a cyclical manner

II.

Two strings are attached in parallel.

Which one of the following statements is ALWAYS correct? (assuming that mass m that is attached to the strings is identical in each experiment)

a) the time-period of one oscillation of the equivalent string is longer than the time-periods of one oscillation of the original strings

b) the frequency of an oscillation of the equivalent string is bigger than the frequency of an oscillation of the original strings.

c) the oscillation amplitude of the equivalent string is larger than the amplitude of an oscillation of the original strings.

d) the equivalent string constant is smaller than the spring constant of the original strings.

e) the lengthening of the equivalent string in the equilibrium state is larger than the lengthening of the separate strings

Please reason your answer with an appropriate calculation.

Answer 1

DIFFERENCE BETWEEN STANDING WAVE AND A PROGRESSIVE WAVE WITHIN A STRING IS AS FOLLOWS:

STANDING WAVES:

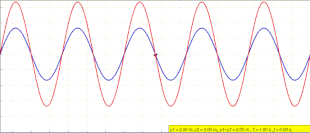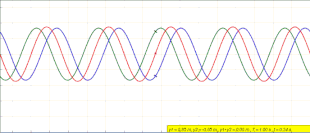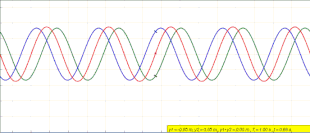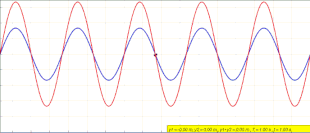
Animation of a standing wave (red) created by the superposition of a left traveling (blue) and right traveling (green) wave

Waves which appear to be vibrating vertically without traveling horizontally. Created from waves with identical frequency and amplitude interfering with one another while traveling in opposite directions.

Standing wave harmonics

A wave that travels down a rope gets reflected at the rope’s end. If the end of the rope is free, then the wave returns right side up. If the end of the rope is fixed, then the wave will be inverted.

Figure 1: A wave pulse reflected from a free end returns right side up. A wave pulse reflecting from a fixed end is inverted.

For a rope with two fixed ends, another wave travelling down the rope will interfere with the reflected wave. At certain frequencies, this produces standing waves where the nodes and antinodes stay at the same places over time. For all standing wave frequencies, the nodes and antinodes alternate with equal spacing.

The lowest frequency (which corresponds with the longest wavelength) that will produce a standing wave has one “bump” (see Figure 2) along the string length L. This standing wave is called the fundamental frequency, with L= and there are two nodes and one antinode.

Figure 2: For the fundamental frequency of a standing wave between two fixed ends, the wavelength is double the length of the string.

Each successive harmonic has an additional node and antinode. For the second harmonic, there are two “bumps”, for the third, there are three, and so on.

HOW TO CREATE A STANDING WAVE:

In general, standing waves can be produced by any two identical waves traveling in opposite directions that have the right wavelength. In a bounded medium, standing waves occur when a wave with the correct wavelength meets its reflection.Standing waves can form under a variety of conditions, but they are easily demonstrated in a medium which is finite or bounded. A phone cord begins at the base and ends at the handset. (Or is it the other way around?) Other simple examples of finite media are a guitar string (it runs from fret to bridge), a drum head (it's bounded by the rim), the air in a room (it's bounded by the walls), the water in Lake Michigan (it's bounded by the shores), or the surface of the Earth (although not bounded, the surface of the Earth is finite).

Standing waves don't form under just any circumstances. They require that energy be fed into a system at an appropriate frequency. That is, when the driving frequency applied to a system equals its natural frequency. This condition is known as resonance. Standing waves are always associated with resonance. Resonance can be identified by a dramatic increase in amplitude of the resultant vibrations. Compared to traveling waves with the same amplitude, producing standing waves is relatively effortless. In the case of the telephone cord, small motions in the hand result will result in much larger motions of the telephone cord.

Progressive Wave:

A progressive wave is defined as the onward transmission of the vibratory motion of a body in an elastic medium from one particle to the successive particle.

Characteristics of progressive wave

(a) Each particle of the medium executes vibration about its mean position. The disturbance progresses onward from one particle to another.

(b) The particles of the medium vibrate with same amplitude about their mean positions.

(c) Each successive particle of the medium performs a motion similar to that of its predecessor along the propagation of the wave, but later in time.

(d) The phase of every particle changes from 0 to 2π.

(e) No particle remains permanently at rest. Twice during each vibration, the particles are momentarily at rest at extreme positions, different particles attain the position at different time.

(f) Transverse progressive waves are characterised by crests and troughs. Longitudinal waves are characterised by compressions and rarefactions.

(g) There is a transfer of energy across the medium in the direction of propagation of progressive wave.

(h) All the particles have the same maximum velocity when they pass through the mean position.

(i) The displacement, velocity and acceleration of the particle separated by mλ are the same, where m is an integer

ANSWER 2 IS:

OR THE CASE BECOMES AS :

HENCE FROM THE ABOVE CALCULATIONS IT IS CLEAR THAT:

) the frequency of an oscillation of the equivalent string is bigger than the frequency of an oscillation of the original strings. is always correct