Question

A) Describe what you think will happen if two cars of equal mass collide with each other but do not stick together. What roles do their respective speeds play in your response? Does it matter what their speeds are? (Be specific)

B) how can you tell whether a collision is elastic or inelastic? What criteria do you use?

Answer 1

The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum after the collision, and is expressed by the equation

Likewise, the conservation of the total kinetic energy is expressed by the equation

These equations may be solved directly to find v_i when u_i are known or vice versa. An alternative solution is to first change the frame of reference such that one of the known velocities is zero. The unknown velocities in the new frame of reference can then be determined and followed by a conversion back to the original frame of reference to reach the same result. Once one of the unknown velocities is determined, the other can be found by symmetry.

Solving these simultaneous equations for v_i we get:

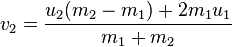
or

.

No it does not matter what their speeds are.

B)

Collisions in which the kinetic energy is also conserved, i.e. in which the kinetic energy just after the collision equals the kinetic energy just before the collision, are called elastic collision. In these collisions no ordered energy is converted into thermal energy. Collisions in which the kinetic energy is not conserved, i.e. in which some ordered energy is converted into internal energy, are called inelastic collisions. If the two objects stick together after the collision and move with a common velocity vf, then the collision is said to be perfectly inelastic.

Note: In collisions between two isolated objects momentum is always conserved.  Kinetic energy is only conserved in elastic collisions. We always have m1v1i + m2v2i = m1v1f + m2v2f. Only for elastic collisions do we also have (1/2)m1v1i2 + (1/2)m2v2i2 = (1/2)m1v1f2 + (1/2)m2v2f2.