Question
In: Physics
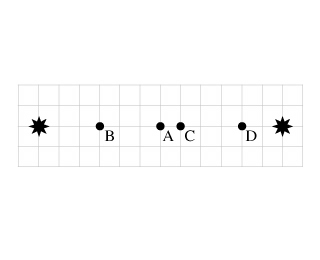
Two sources of coherent radio waves broadcasting in phase arel ocated as shown below. Each grid...

|
|
|
|
Solutions
Expert Solution
The concepts of coherence, path difference, constructive and destructive interference are required to solve the problem.
First, find the distance of the given point from each source. Then, calculate the difference between the two distances. Finally, use the condition of constructive and destructive interference and determine whether the interference is constructive or destructive.
The path difference between the two interfering waves is given as,
Here, is the distance of the point from one source and is the distance of the same point from the second source
The condition for interference is,
Here, is the wavelength of the two sources.
For constructive interference, the value of m is the integral multiple of wavelength. That is,
Here, n is the order of pattern.
For destructive interference n is given as,
(1)
Distance of the point A from the left source is,
Here, a is the length of the one square grid.
Distance of the point A from the right source is,
The path difference between the two interfering waves is given as,
Substitute 6a for and in the above equation .
The condition for interference is,
Replace m with n.
Rearrange the equation for m.
Substitute 0 for in the above equation.
The path difference is the integral multiple of the wavelength. Hence, the interference between the two waves at point A is constructive.
(2)
Distance of the point B from the left source is,
Here, a is the length of the one square grid.
Distance of the point B from the right source is,
The path difference between the two interfering waves is given as,
Substitute 3a for and 9a for in the above equation .
Substitute 0.5 m for a in the above equation .
The condition for interference is,
Rearrange the equation for n.
Substitute 3.0 m for and 2.0 m for in the above equation.
The above obtained value is matching with the term and so, this interference can be considered as destructive interference.
If the path difference is equal to odd integral multiple of half of the wavelength then the interference is destructive. Therefore, the interference between the two waves at point B is destructive.
(3)
Distance of the point C from the left source is,
Here, a is the length of the one square grid.
Distance of the point C from the right source is,
The path difference between the two interfering waves is given as,
Substitute 7a for and 5a for in the above equation .
Substitute 0.5 m for a in the above equation .
Rearrange the equation for n.
Substitute 1.0 m for and 2.0 m for in the above equation.
The above obtained value is matching with the term and so, this interference can be considered as destructive interference.
If the path difference is equal to odd integral multiple of half of the wavelength then the interference is destructive. Therefore, the interference between the two waves at point C is destructive.
(4)
Distance of the point D from the left source is,
Here, a is the length of the one square grid.
Distance of the point C from the right source is,
The path difference between the two interfering waves is given as,
Substitute 10a for and 2a for in the above equation .
Substitute 0.5 m for a in the above equation .
The condition for interference is,
Replace m with n.
Rearrange the equation for m.
Substitute 4.0 m for and 2.0 m for in the above equation.
This implies that the path difference is an integral multiple of wavelength. Therefore, the interference between the two waves at point D is constructive.
Ans: Part 1At point A, the interference between the two waves is constructive.
Part 2At point B, the interference between the two waves is destructive.
Part 3At point C, the interference between the two waves is destructive.
Part 4At point D, the interference between the two waves is constructive.
Related Solutions
Two sources emit electromagnetic waves that are coherent and in phase. To reach point P, the...
10) Two coherent sources emit waves that have a wavelength of 0.44 m. Determine whether constructive...
Two speakers spaced a distance 1.5 m apart emit coherent sound waves at a frequency of 680 Hz in all directions. The waves start out in phase with each other.
If two sinusoidal waves with amplitudes 4A and 8A are in phase with each other, their...
Coherent electromagnetic waves with wavelength λ=500nm pass through two identical slits. The width of each slit...
Standing waves are set up on two strings fixed at each end, as shown in the...
Standing waves are set up on two strings fixed at each end, as shown in the...
Two radio antennas separated by d = 272 m as shown in the figure below simultaneously...
Public Radio station KXPR-FM in Sacramento broadcasts at 88.9 MHz. The radio waves pass between two...
Two speakers spaced emitting identical sound waves in phase with each other of wavelength 1.00 m...
- The score recorded for student 12 for event 5 is incorrect. The score should be a...
- Formulate the outline of a precision pricing policy for a four-star hotel designed to accommodate business...
- The chosen Company is Amazon. Financial statements for the years 2016, 2017 and 2018. A. Analyze...
- With the establishment of the World Trade Organization (WTO) in 1995 (previously General Agreement on Tariffs...
- The London Private Hospital has 3 patient services departments – Adult Medicine, Obstetrics and Paediatrics. It...
- Suppose that an initially empty queue performs the following operations. enqueue(7), enqueue(3), dequeue(), front(), enqueue(8), enqueue(5),...
- Write a program that manages a list of patients for a medical office. Patients should be...
 genius_generous answered 3 years ago
genius_generous answered 3 years ago