Question

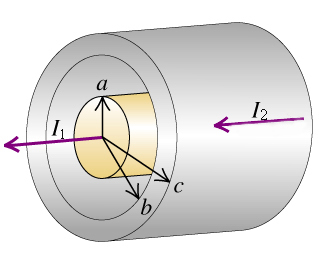
A solid conductor with radius a is supported by insulating disks on the axis of a conducting tube with inner radius b and outer radius c( (Intro 1 figure) ). The central conductor and tube carry currents and correspondingly in the same direction. The currents are distributed uniformly over the cross sections of each conductor.Derive an expression for the magnitude of the magnetic field

A) at points outside the central, solid conductor but inside the tube Express your answer in terms of the variables , , (), and appropriate constants ( and ).

b) at points outside the tube

Express your answer in terms of thevariables , , (), and appropriate constants ( and ).

Answer 1

Concepts and reason

The concept required to solve this problem is the Ampere’s law and the magnetic field.

Initially, write the Ampere’s law for the points outside the central, solid conductor but inside the tube. Then, rearrange the expression for the magnetic field. Later, write the ampere law for the points outside the tube and finally, rearrange the expression for the magnetic field.

Fundamentals

The expression of the Ampere’s law is,

$\int {\vec B \cdot d\vec l} = {\mu _0}I$

Here, $\vec B$ is the magnetic field, $d\vec l$ is the line element, ${\mu _0}$ is the permittivity, and I is the current.

(a)

The expression of the Ampere’s law for the points outside the central, solid conductor but inside the tube is,

$\begin{array}{c}\\\int {\vec B \cdot d\vec l} = {\mu _0}{I_1}\\\\\int {Bdl\cos \theta } = {\mu _0}{I_1}\\\end{array}$

Substitute $0^\circ$ for $\theta$ and solve.

$\begin{array}{c}\\\int {Bdl\cos 0^\circ } = {\mu _0}{I_1}\\\\B\int {dl} = {\mu _0}{I_1}\\\end{array}$

Integrate over the line element and substitute $2\pi r$ for l.

$\begin{array}{c}\\B\int {dl} = {\mu _0}{I_1}\\\\Bl = {\mu _0}{I_1}\\\\B\left( {2\pi r} \right) = {\mu _0}{I_1}\\\\B = \frac{{{\mu _0}{I_1}}}{{2\pi r}}\\\end{array}$

(b)

The expression of the Ampere’s law for the points outside the tube is,

$\begin{array}{c}\\\int {\vec B \cdot d\vec l} = {\mu _0}\left( {{I_1} + {I_2}} \right)\\\\B\int {dl} = {\mu _0}\left( {{I_1} + {I_2}} \right)\\\end{array}$

Integrate over the line element and substitute $2\pi r$ for l.

$\begin{array}{c}\\B\int {dl} = {\mu _0}\left( {{I_1} + {I_2}} \right)\\\\Bl = {\mu _0}\left( {{I_1} + {I_2}} \right)\\\\B\left( {2\pi r} \right) = {\mu _0}\left( {{I_1} + {I_2}} \right)\\\\B = \frac{{{\mu _0}\left( {{I_1} + {I_2}} \right)}}{{2\pi r}}\\\end{array}$

Ans: Part a

The magnetic field for the points outside the central, solid conductor but inside the tube is$\frac{{{\mu _0}{I_1}}}{{2\pi r}}$.

Part b

The magnetic field outside the tube is $\frac{{{\mu _0}\left( {{I_1} + {I_2}} \right)}}{{2\pi r}}$.