Question

In a school district, all sixth grade students take the same standardized test. The superintendant of the school district takes a random sample of 2323 scores from all of the students who took the test. She sees that the mean score is 147147 with a standard deviation of 18.963118.9631. The superintendant wants to know if the standard deviation has changed this year. Previously, the population standard deviation was 1212. Is there evidence that the standard deviation of test scores has increased at the α=0.01α=0.01 level? Assume the population is normally distributed.

Step 2 of 5 :

Determine the critical value(s) of the test statistic. If the test is two-tailed, separate the values with a comma. Round your answer to three decimal places.

Step 3 of 5: Determine the value of the test statistic. Round your answer to three decimal places.

Step 4 of 5: Make the decision

Step 5 of 5: What is the conclusion?

Answer 1

Solution:

Given ,

n = 23

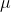= 18, 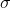² = 0.1

, s = 0.5951

Step 1 of 5: State the hypotheses in terms of the standard deviation

H0 :   = 12

Ha : > 12

Step 2 of 5: Determine the critical value(s) of the test statistic.

d.f. = n - 1 = 23 - 1 = 22

Here , RIGHT Tailed test.

So the critical values is

α=0.01 , df = 22

Using chi square table ,

the critical values is 40.289

Step 3 of 5: Determine the value of the test statistic.

The test statistic is

² = (n - 1)s²/²

= (23 - 1) (18.9631)²/(12²)

=  54.939

the value of the test statistic is 54.939

Step 4 of 5: Make the decision.

Rejection region is > 40.289

Here , 54.939 > 40.289

So , Reject Null Hypothesis

Step 5 of 5: What is the conclusion?

Yes , there is sufficient evidence to support the claim that the standard deviation of test scores has increased