Question
In: Physics
) A 1.53-kg bucket hangs on a rope wrapped around a pulley of mass 7.07 kg...
) A 1.53-kg bucket hangs on a rope wrapped around a pulley of mass 7.07 kg and radius 66 cm. This pulley is frictionless in its axle, and has the shape of a solid uniform disk. After the bucket has been released, what is the angular acceleration of the pulley?
Solutions
Expert Solution
Gravitational acceleration = g = 9.81 m/s2
Mass of the bucket = m = 1.53 kg
Mass of the pulley = M = 7.07 kg
Radius of the pulley = R = 66 cm = 0.66 m
Moment of inertia of the pulley = I
I = MR2/2
I = (7.07)(0.66)2/2
I = 1.54 kg.m2
Tension in the rope = T
Angular acceleration of the pulley = 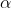
Acceleration of the bucket = a
a = 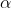 R
R
For the bucket,
ma = mg - T
T = mg - ma
T = m(g - 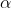 R)
R)
For the pulley,
I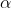 = TR
= TR
I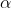 = m(g -
= m(g -
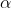 R)R
R)R
(1.54)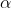 =
(1.53)(0.66)(9.81 - 0.66
=
(1.53)(0.66)(9.81 - 0.66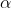 )
)
1.54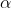 = 9.906 -
0.666
= 9.906 -
0.666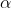
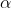 = 4.489
rad/s2
= 4.489
rad/s2
Angular acceleration of the pulley = 4.489 rad/s2
Related Solutions
A bucket of water of mass 16.0 kg is suspended by a rope wrapped around a...
A rope of negligible mass hangs vertically on each side of a pulley. The pulley, which...
A rope of negligible mass is wrapped around a 225-kg solid cylinder of radius 0.400 m....
A lightweight rope is wrapped around a 100-lb drum, passes over a frictionless pulley, and is...
A rope is wrapped around the rim of a large uniform solid disk of mass 155...
a bucket of water with total mass 20 kg is attached to. a rope, which in...
A 3.2 kg box hangs on a rope without mass and that does not stretch, the...
A string is wrapped around a pulley with a radius of 2.0 cm and no appreciable...
A 61.0 kg box hangs from a rope. What is the tension in the rope if:...
A 55.0 kg box hangs from a rope. What is the tension in the rope if:...
- plot this data into a bar graph: PYTHON data=pandas.read_csv(r'data/tv_shows.txt', low_memory=False) print((data)) print((data.columns)) TV Shows : Rating...
- At 25 degrees celsius only .0640 mol of the generic salt AB2 is soluble in 1.00...
- cite 3 most important healthcare financing concern in the united states today and how expenses and...
- S Company reported the following account balances on its After Closing Trial Balance
- A.) A 700- kg car collides with a 1300- kg car that was initially at rest...
- My industry is Optometry: 7. What are the impacts of the macroeconomic business cycle on demand...
- Compute Bond Proceeds, Amortizing Discount by Interest Method, and Interest Expense Boyd Co. produces and sells...
 genius_generous answered 2 years ago
genius_generous answered 2 years ago