Question

Given a grammar G, G = (Ν, Σ, Π, S), where

Ν = { ... }

Σ = { ... }

Π = { ... }

S is ... For a string ... write

(a) A leftmost derivation

(b) A rightmost derivation

Answer 1

Leftmost derivation
• Leftmost nonterminal is replaced in each step
Rightmost derivation
• Rightmost nonterminal is replaced in each step
Example
• Grammar
S → AB, A → a, B → b
• Leftmost derivation for ab-

S ⇒ AB ⇒ aB ⇒ ab
• Rightmost derivation for ab-

S ⇒ AB ⇒ Ab ⇒ ab

For unambiguous

Consider the following grammar-

S → aS / ∈

The language generated by this grammar is-

L = { aⁿ , n>=0 } or a*

All the strings generated from this grammar have their leftmost derivation and rightmost derivation exactly same.

Let us consider a string w = aaa.

Leftmost Derivation-

S → aS

→ aaS (Using S → aS)

→ aaaS (Using S → aS)

→ aaa∈

→ aaa

Rightmost Derivation-

S → aS

→ aaS (Using S → aS)

→ aaaS (Using S → aS)

→ aaa∈

→ aaa

Clearly,

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

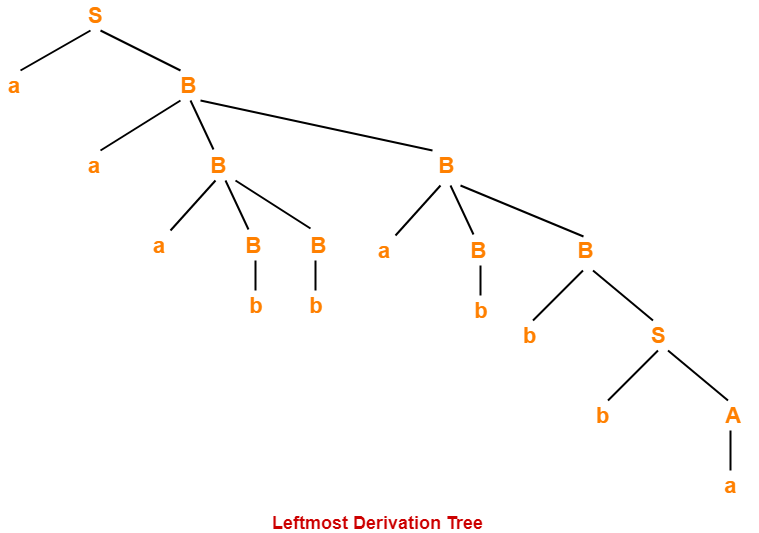
Now, let us derive the string w using leftmost derivation.

Leftmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaaBBB (Using B → aBB)

→ aaabBB (Using B → b)

→ aaabbB (Using B → b)

→ aaabbaBB (Using B → aBB)

→ aaabbabB (Using B → b)

→ aaabbabbS (Using B → bS)

→ aaabbabbbA (Using S → bA)

→ aaabbabbba (Using A → a)

2. Rightmost Derivation-

• The process of deriving a string by expanding the rightmost non-terminal at each step is called as rightmost derivation.
• The geometrical representation of rightmost derivation is called as a rightmost derivation tree.

Example-

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

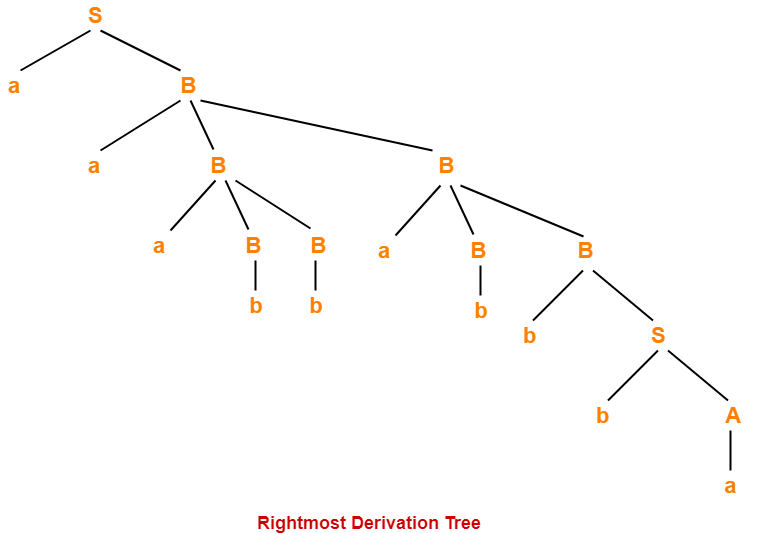
Now, let us derive the string w using rightmost derivation.

Rightmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaBaBB (Using B → aBB)

→ aaBaBbS (Using B → bS)

→ aaBaBbbA (Using S → bA)

→ aaBaBbba (Using A → a)

→ aaBabbba     (Using B → b)

→ aaaBBabbba (Using B → aBB)

→ aaaBbabbba    (Using B → b)

→ aaabbabbba (Using B → b)

NOTES For unambiguous grammars, Leftmost derivation and Rightmost derivation represents the same parse tree. For ambiguous grammars, Leftmost derivation and Rightmost derivation represents different parse trees.

Here,

• The given grammar was unambiguous.
• That is why, leftmost derivation and rightmost derivation represents the same parse tree.