Question

the following are impulse responses/outputs of discrete -time LTI systems. Determine whether each system is causal and/or stable. justify your answers
1. h [n] = 1/5^n u [n]
2. h [n] = 5^n u [3-n]
3. y [n] = 3x [n] - 0.15y [n-1]
4. y [n] = 2e^-x [n]
5. y [n] = n^2 4x [n]

B. Show if the systems defined in 1 to 5 above have bounded input and output (BIBO) from the summation of their impulse responses for n = 0, 1,2,3,4.

Answer 1

1) is causal because it is depending only on present value of input

And stable because for bounded input it will give bounded output

Let n = 3

Then h(3) = (1/5)^64 = 0.008 it means if we put finite input it will give finite output.

2)it is not a causal system because output is depending futurevalue of input

Let n = 0, so U(3-0) = U(3)

It is stable because for any finite value it will give finite input

3)

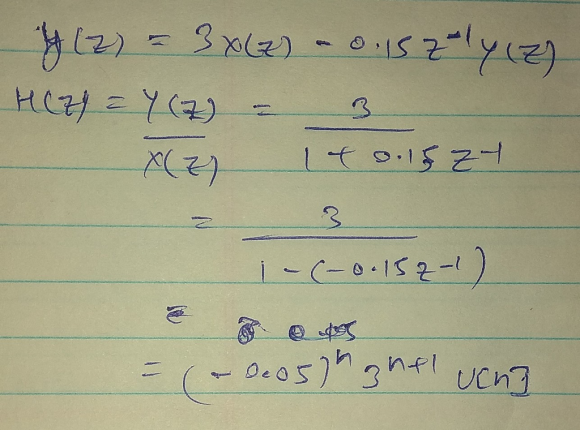
it is non causal because for n=0

3^(1) it means it is depending on future value

But it is stable because for any finite input we will get finite output

4) it is causal because output is dependending on present value and stable because for any finite input it will give finite output

5)h[n]=4*n^2 it is also causal and stable same reason as part 4)

B)

4) when we know x[n] and then we put values of n we will get finite output because x[n] is in the power of exponentially decreasing function which will always give finite value

5)you can check yourself by putting value of n

h[n] = 4*n^2