Question

Problem 1) The reputations (and hence sales) of many businesses can be severely damaged by shipments of manufactured items that contain a large percentage of defectives. For example, a manufacturer of alkaline batteries may want to be reasonably certain that fewer than 6% of its batteries are defective. Suppose a random sample of 800 batteries are selected from a very large shipment; each is tested and 31 defective batteries are found. (The manufacturer is analyzing the proportion of DEFECTIVE batteries.)

a) Consider just one experimental unit – that is, one battery. What is the response variable for that one battery? Categorical or quantitative?

b) The manufacturer wants to conduct a significance test to decide if there is sufficient evidence for the manufacturer to conclude that the fraction defective in the entire shipment is less than 6 percent. Verify the conditions for using the normal approximation for the sample proportion.

c) Conduct the significance test. Keep two nonzero digits in your calculation for ?̂ and for the standard deviation. Sketch the distribution for ??̂ showing mean and area for P-value. State your conclusion in plain English in the context of the problem: choose one of the statements for your conclusion, depending on your P-value:

• We have evidence to show that the fraction defective in the entire shipment is less than 6 percent (P-value = _______) • We do not have evidence to show that the fraction defective in the entire shipment is less than 6 percent.

Answer 1

(a)

The response to one battery is either defective or non-defective and hence the response variable is categorical.

(b)

Here tha sample size is 800, which is large enough for us to apply the normal approximation to sample proportion.

(c)

Here the null and alternative hypotheses are given by

The test statistic is given by

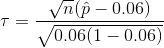
From the sample , it is observed that n=800,

The standard deviation is given by

The p-value , obtained from the Biometrika table, is very low and less than 0.05. Hence we reject the null at 5% level of significance and hence we have enough evidence to show that the fraction defective in the entire shipment is less than 6 percent.(0.000003)

Hopefully this will help you. In case of any query, do comment. If you are satisfied with the answer, give it a like. Thanks.