Question

Suppose x has a distribution with μ = 27 and σ = 19.

(a) If a random sample of size n = 39 is drawn, find μx, σ x and P(27 ≤ x ≤ 29). (Round σx to two decimal places and the probability to four decimal places.) μx = σ x = P(27 ≤ x ≤ 29) =

(b) If a random sample of size n = 64 is drawn, find μx, σ x and P(27 ≤ x ≤ 29). (Round σ x to two decimal places and the probability to four decimal places.) μx = σ x = P(27 ≤ x ≤ 29) =

(c) Why should you expect the probability of part (b) to be higher than that of part (a)? (Hint: Consider the standard deviations in parts (a) and (b).)

The standard deviation of part (b) is part (a) because of the sample size. Therefore, the distribution about μx is .

Answer 1

Solution :

Given that,

mean = = 27

standard deviation = = 19

a) n = 39

=   = 27

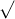= / n = 19 / 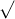39 = 3.04

  P(27 29)  

= P[(27 - 27) /3.04 ( - ) / (29 - 27) / 3.04 )]

= P(0 Z 0.66 )

= P(Z 0.66) - P(Z 0)

Using z table,  

  = 0.7454 - 0.5  

= 0.2454

b) n = 64

=   = 27

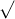= / n = 19 / 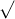64 = 2.38

  P(27 29)  

= P[(27 - 27) /2.38 ( - ) / (29 - 27) / 2.38)]

= P(0 Z 0.84 )

= P(Z 0.84) - P(Z 0)

Using z table,  

  = 0.7995 - 0.5  

= 0.2995

c) The standard deviation of part (b) is smaller than part (a) because of the sample size is larger. Therefore, the distribution about μx is wider