Question

Two chemical companies can supply a raw material. The concentration of an element in this material is important. A random sample with 9 observations from company 1 yields a sample mean of 12.6 and a sample standard deviation of 2.7, and another sample with 11 observations from company 2 yields a sample mean of 14.5 and a sample standard deviation of 5.5. Is there a sufficient evidence to conclude that the variance of company 1 is less than variance of company 2 at 5% significance level?

Answer 1

Solution:

The null and alternative hypothesis are

H₀ : ₁² =  ₂²​​  

H_a :  ₁² <  ₂²​​  

< sign in H_a indicates that left tailed test.

1) Critical value in this case is F_{1-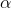 , df1,df2}

d.f.₁ = n₁ - 1 = 9 - 1 = 8

n₂ = n₂ - 1 = 11 - 1 = 10

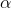= 5% = 0.05

1 - 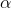= 0.95

So , critical value is F_0.99,8,10 = 0.2988

(Use F Table )

Now ,

The test statistic is

F = s₁²/s₂² = 2.7²/5.5² = 0.2410

F = 0.2410 < F_0.99,8,10 = 0.2988

So , test statistic falls in the rejection region.

We reject the null hypothesis at 5% level of significance .

YES , There is sufficient evidence to conclude that the variance of company 1 is less than variance of company 2 at 5% significance level.