Question

In one of the studies, it was found that, in a random sample of 261 married persons, 135 were smokers while in a sample of 239 non-married persons there were 131 smokers.

a. Find a 90% confidence interval for the true difference in proportion of smokers among the married and non-married populations.

b. Based on the above interval, can one conclude that there is a significant difference between the proportions of smokers in the two populations? Justify your answer

c. Do a formal hypothesis testing to test whether the two populations proportions are significantly different. Use ? = 0.10 and a p-value method. Set up the appropriate null and alternative hypotheses. Is the conclusion same as the one in part(b)?

Answer 1

(a)

n1 = 261

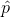1 = 135/261 = 0.5172

n2 = 239

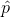2 = 131/239 = 0.5481

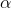= 0.10

From Table, critical values of Z = 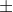1.64

Confidence Interval:

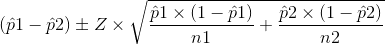
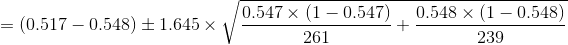
= ( - 0.104, 0.043)

So,

Answer is:

( - 0.104, 0.043)

(b)

Since the confidence interval ( - 0.104, 0.043) contains 0, one cannot conclude that there is a significant difference between the proportions of smokers in the two populations

(c)

H0:Null Hypothesis: p1 = p2 ( the two populations proportions are not significantly different)

HA: Alternative Hypothesis: p1 p2 ( the two populations proportions are significantly different) (Claim)

n1 = 261

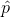1 = 135/261 = 0.5172

n2 = 239

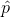2 = 131/239 = 0.5481

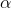= 0.10

From Table, critical values of Z = 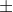1.64

Pooled Proportion is given by:

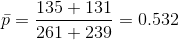
Test Statistic is given by:

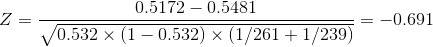
By Technology,

P - Value = 0.4875

Since P - Value = 0.4875 isgreater than 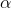= 0.10, the difference is not significant.Fail to reject null hypothesis.

Conclusion:
The data do not support the clim that the two populations proportions are significantly different.

The conclusion is same as the one in part(b).