Question
In: Statistics and Probability
A dietician read in a survey that 82.04% of adults in the U.S. do not eat...
A dietician read in a survey that 82.04% of adults in the U.S.
do not eat breakfast at least 2 days a week. She believes that a
smaller proportion skip breakfast 2 days a week. To verify her
claim, she selects a random sample of 77 adults and asks them how
many days a week they skip breakfast. 49 of them report that they
skip breakfast at least 2 days a week. Test her claim at αα =
0.01.
The correct hypotheses would be:
- H0:p≤0.8204H0:p≤0.8204
HA:p>0.8204HA:p>0.8204 (claim) - H0:p≥0.8204H0:p≥0.8204
HA:p<0.8204HA:p<0.8204 (claim) - H0:p=0.8204H0:p=0.8204
HA:p≠0.8204HA:p≠0.8204 (claim)
Since the level of significance is 0.01 the critical value is
-2.326
The test statistic is: (round to 3 places)
The p-value is: (round to 3 places)
The decision can be made to:
- reject H0H0
- do not reject H0H0
The final conclusion is that:
- There is enough evidence to reject the claim that a smaller proportion skip breakfast 2 days a week.
- There is not enough evidence to reject the claim that a smaller proportion skip breakfast 2 days a week.
- There is enough evidence to support the claim that a smaller proportion skip breakfast 2 days a week.
- There is not enough evidence to support the claim that a smaller proportion skip breakfast 2 days a week.
Solutions
Expert Solution
The correct hypothesis would be:
H0: p ≥ 0.8204 against HA : p < 0.8204 (claim)
-----------------------------------------------------------------------------------------------------------------------------------
Here 

 (sample
size)
(sample
size)
 (number of
adults skip breakfast at least 2 days a week)
(number of
adults skip breakfast at least 2 days a week)
 (significance level)
(significance level)
 (critical value)
(critical value)
Sample proportion is,

The test statistic is:



----------------------------------------------------------------------------------------------------------------------------------
The p-value = 0
-----------------------------------------------------------------------------------------------------------------------------------
- Since Z = -4.207 < Z
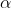 = -2.326,
we can conclude that the null hypothesis is rejected.
= -2.326,
we can conclude that the null hypothesis is rejected. - Using p-value approach, since p-value <
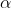 ,we can
conclude that the null hypothesis is rejected.
,we can
conclude that the null hypothesis is rejected.
 The decision
can be made to: Reject H0
The decision
can be made to: Reject H0
-------------------------------------------------------------------------------------------------------------------------------------
The final conclusion is that:
There is enough evidence to support the claim that a smaller proportion skip breakfast 2 days a week.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Related Solutions
A dietician read in a survey that 63.3% of adults in the U.S. do not eat...
According to a survey, 16% of U.S. adults with online services currently read e-books. Assume that...
Assume that 20% of U.S. adults subscribe to the "five-second rule." That is, they would eat...
A study claims 32% of U.S. adults eat chocolate daily. A researcher suspects the actual percentage...
3. a. A survey of 1000 U.S. adults found that 34% of people said that they...
In a survey of 500 U.S. adults, 45% of them said that lounging at the beach...
A survey of 1383 U.S. adults is taken to measure support for increasing federal funding for...
According to one survey, the mean serum cholesterol level for U.S. adults was 203.5 , with...
In a survey of U.S. adults with a sample size of 2040, 315 said Franklin Roosevelt...
a random survey of 1000 U.S. adults in 2007, 570 said it is likely that life...
- plot this data into a bar graph: PYTHON data=pandas.read_csv(r'data/tv_shows.txt', low_memory=False) print((data)) print((data.columns)) TV Shows : Rating...
- At 25 degrees celsius only .0640 mol of the generic salt AB2 is soluble in 1.00...
- cite 3 most important healthcare financing concern in the united states today and how expenses and...
- S Company reported the following account balances on its After Closing Trial Balance
- A.) A 700- kg car collides with a 1300- kg car that was initially at rest...
- My industry is Optometry: 7. What are the impacts of the macroeconomic business cycle on demand...
- Compute Bond Proceeds, Amortizing Discount by Interest Method, and Interest Expense Boyd Co. produces and sells...
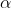 = -2.326,
we can conclude that the null hypothesis is rejected.
= -2.326,
we can conclude that the null hypothesis is rejected. orchestra answered 2 years ago
orchestra answered 2 years ago