Question

The data below are the final exam scores of 10 randomly selected calculus students and the number of hours they slept the night before the exam:

Hours Slept (x)	7	11	6	13	7	8	8	11	12	9
Exam Scores (y)	68	83	63	91	69	81	88	93	93	74

Using the equation of the regression line, with all numbers in it rounded to 2 decimal places, predict the final exam score of a student who slept for 3 hours the night before the exam. (Round the score to 2 decimal places)

Select one:

49.83

45.64

55.97

50.22

59.58

61.01

Answer 1

Solution:

n = 10

	X	Y	XY	X^2	Y^2
	7	68	476	49	4624
	11	83	913	121	6889
	6	63	378	36	3969
	13	91	1183	169	8281
	7	69	483	49	4761
	8	81	648	64	6561
	8	88	704	64	7744
	11	93	1023	121	8649
	12	93	1116	144	8649
	9	74	666	81	5476
SUM	92	803	7590	898	65603

Slope of the regression line is

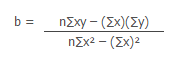
   b = 3.92

Now , y intercept of the line is

   a = 44.21

The equation of the regression line is

= a + bx

i.e. =  44.21 + (3.92)x

For x = 3, find the predicted value of y .

Put x = 3  in the regression line equation.

= 44.21 + (3.92 * 3) = 55.97

Answer : 55.97