Question

A researcher is looking at the relationships between age and the number of instances of shoplifting. Use the data below to establish hypotheses and calculate the correlation for the relationship between age and shoplifting. State and explain your decision with regard to whether the H₀ is ultimately rejected or accepted.

Age (X)	Number of Times Shoplifted (Y)
18	12
20	10
18	10
19	11
40	4
30	3
27	3
21	8
19	7

Answer 1

Solution:

Null and alternative hypothesis are

H₀: = 0 vs H₁ :    0

n = 9

	X	Y	XY	X^2	Y^2
	18	12	216	324	144
	20	10	200	400	100
	18	10	180	324	100
	19	11	209	361	121
	40	4	160	1600	16
	30	3	90	900	9
	27	3	81	729	9
	21	8	168	441	64
	19	7	133	361	49
Sum	212	68	1437	5440	612

Putting values

r = -0.787

Now ,

n = 9

df = n - 2 = 9 - 2 = 7

Take 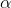= 0.05

Using the critical value table for Pearson correlation coefficient, (two tailed )

Critical value are 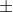 0.666

r = -0.787

| r | = | -0.787| = 0.787

r >  0.666

reject H₀

significance correlation.

YES , there is sufficient evidence to conclude that there is a linear correlation between the two​ variables.