Question

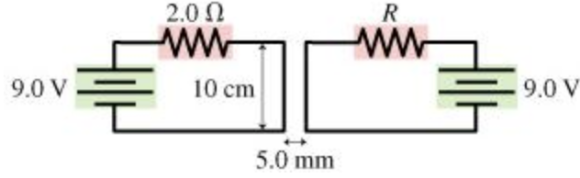The two 10-cm-long parallel wires in the figure are separated by 5.0 mm. For what value of the resistor R will the force between the two wires be 1.1×10⁻⁴ N ?

Answer 1

Concepts and reason

The concepts of magnetic force between two parallel wires and Ohm's law are required to solve the problem. First, determine the current flowing through the left side wire by using Ohm's law. Then determine the current flowing through the right-side circuit by using the relation of magnetic force between two parallel wires. Finally, calculate the value of resistance by using Ohm's law.

Fundamentals

According to Ohm's law current passing through a conductor is directly proportional to the voltage across the conductor. The expression for Ohm's law is given as, \(I=\frac{V}{R}\)

Here, \(\mathrm{V}\) is the voltage across the conductor, and \(\mathrm{R}\) is the resistance. Magnetic force between two current carrying parallel wires of length \(l\) is given as, \(F=\frac{\mu_{0} I_{1} I_{2} l}{2 \pi r}\)

Here, \(I_{1}\) and \(I_{2}\) are the currents in the two wires, \(r\) is the distance between the two wires, and, \(\mu_{0}\) is the permeability of free space.

Consider the left side circuit and use Ohm's law.

The current flowing in the left side wire is determined by using the equation, \(I_{1}=\frac{V_{1}}{R_{1}}\)

Substitute \(9.0 \mathrm{~V}\) for \(V_{1}\) and \(2.0 \Omega\) for \(R_{1}\) in the above equation.

\(I_{1}=\frac{9.0 \Omega}{2.0 \mathrm{~V}}\)

\(=4.5 \mathrm{~A}\)

According to Ohm's law current passing through a conductor is directly proportional to the voltage across the conductor. The current flowing in the left side circuit is determined by dividing voltage across the resistor by the resistance.

Consider the right-side circuit and determine the value of the resistor R. Magnetic force between the two parallel wires is given as, \(F=\frac{\mu 0 I 1 I 2 l}{2 \pi r}\)

Here, \(I_{1}\) is the current in the left side wire, \(I_{2}\) is the current in the right-side wire, \(r\) is the distance between the two wires, and \(\mu_{0}\) is the permeability of free space. Rearrange the above equation for \(I_{2}\). \(I_{2}=\frac{2 \pi r F}{\mu_{0} I_{1} l}\)

According to Ohm's law, current flowing in the right-side wire is given as, \(I_{2}=\frac{V_{2}}{R}\)

Here, \(V_{2}\) is the voltage across the resistor \(\mathrm{R}\). Substitute \(\frac{2 \pi r F}{\mu_{0} I_{1} l}\) for \(I_{2}\) in equation \(I_{2}=\frac{V_{2}}{R}\) and rearrange the equation for \(\mathrm{R}\)

$$ \begin{array}{l} \frac{2 \pi r F}{\mu_{0} I_{1} l}=\frac{V_{2}}{R} \\ R=\frac{V_{2} \mu 0 I 1 l}{2 \pi r F} \end{array} $$

Substitute \(9.0 \mathrm{~V}\) for \(V_{2}, 4.5 \mathrm{~A}\) for \(I_{1}, 10 \mathrm{~cm}\) for \(1,4 \pi \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} / \mathrm{A}\) for \(\mu_{0}, 5.0 \mathrm{~mm}\) for \(r\), and \(1.1 \times 10^{-4} \mathrm{~N}\) for \(\mathrm{F}\)

in equation \(R=\frac{V_{2} \mu_{0} I_{1} l}{2 \pi r F}\)

$$ \begin{array}{c} R=\frac{(9.0 \mathrm{~V})\left(4 \pi \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} / \mathrm{A}\right)(4.5 \mathrm{~A})\left(10 \mathrm{~cm}\left(\frac{10^{-2} \mathrm{~m}}{1 \mathrm{~cm}}\right)\right)}{2 \pi\left(5.0 \mathrm{~mm}\left(10^{-3} \mathrm{~m}\right)\right)\left(1.1 \times 10^{-4} \mathrm{~N}\right)} \\ =1.5 \Omega \end{array} $$

The value of the resistor \(\mathrm{R}\) is \(1.5 \Omega\).

The magnetic force between the two current-carrying wires is directly proportional to the current flowing in the two wires and the length of the wires, and inversely proportional to the distance between the two wires. The current flowing in the right-side wire is determined by using the magnetic force between the two wires and then by using Ohm's law the value of resistor \(\mathrm{R}\) is determined.

The value of the resistor \(\mathrm{R}\) is \(1.5 \Omega\).