Question

In: Statistics and Probability

A national air traffic control system handled an average of 47,651 flights during 28 randomly selected...

A national air traffic control system handled an average of 47,651 flights during 28 randomly selected days in a recent year. The standard deviation for this sample is 6,496 flights per day. Complete parts a through c below.

a. Construct a 99​% confidence interval to estimate the average number of flights per day handled by the system.

The 99​% confidence interval to estimate the average number of flights per day handled by the system is from a lower limit of_______ to an upper limit of ___________ .

A national air traffic control system handled an average of 47,132 flights during 29 randomly selected days in a recent year. The standard deviation for this sample is 6,168 flights per day. Complete parts a through c below.


a. Construct a 99​% confidence interval to estimate the average number of flights per day handled by the system.
The 99​% confidence interval to estimate the average number of flights per day handled by the system is from a lower limit of ____________ to an upper limit of____________

Solutions

Expert Solution


Solution :

a ) Given that,

= 47,651

s = 6,496

n = 28

Degrees of freedom = df = n - 1 = 28 - 1 = 27

At 99% confidence level the t is ,

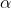= 1 - 99% = 1 - 0.99 = 0.01

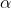/ 2 = 0.01 / 2 = 0.005

t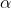 /2,df = t0.005,27 =2.771

Margin of error = E = t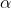/2,df * (s /n)

= 2.771 * (6,496/ 28)

= 3401.76

Margin of error = 3401.76

The 99% confidence interval estimate of the population mean is,

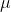- E < < + E

47,651 - 3401.76< 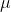< 47,651 +3401.76

44249.24 < 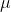< 51052.76

upper limit of =51052.76

lower limit of = 44249.24

b ) Given that,

= 47,132

s =  6,168

n = 29

Degrees of freedom = df = n - 1 = 29 - 1 = 28

At 99% confidence level the t is ,

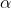= 1 - 99% = 1 - 0.99 = 0.01

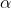/ 2 = 0.01 / 2 = 0.005

t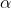 /2,df = t0.005,28 =2.763

Margin of error = E = t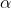/2,df * (s /n)

= 2.763 * ( 6,168 / 29)

= 3164.65

Margin of error = 3164.65

The 99% confidence interval estimate of the population mean is,

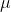- E < < + E

47,132 - 3164.65 < 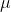< 47,132 + 3164.65

43967.34 < 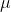< 50296.65

upper limit of =50296.65

lower limit of = 43967.34

orchestra answered 1 year ago
Next > < Previous

Related Solutions

A national air traffic control system handled an average of 47,849 flights during 28 randomly selected...
A national air traffic control system handled an average of 47,849 flights during 28 randomly selected days in a recent year. The standard deviation for this sample is 6,395 flights per day. Complete parts a through c below. a. Construct a 99​% confidence interval to estimate the average number of flights per day handled by the system. The 99​% confidence interval to estimate the average number of flights per day handled by the system is from a lower limit of...
A national air traffic control system handled an average of 47,285 flights during 29 randomly selected...
A national air traffic control system handled an average of 47,285 flights during 29 randomly selected days in a recent year. The standard deviation for this sample is 6,293 flights per day. The 99% confidence interval to estimate the average number of flights per day handled by the system is from Question 7 options: a lower level of 54,223 to an upper level of 66,728. a lower level of 44,056 to an upper level of 50,514. a lower level of...
A national air traffic control system handled an average of 47 comma 474 flights during 28...
A national air traffic control system handled an average of 47 comma 474 flights during 28 randomly selected days in a recent year. The standard deviation for this sample is 6 comma 376 flights per day. Complete parts a through c below. a. Construct a 99 ​% confidence interval to estimate the average number of flights per day handled by the system. The 99 ​% confidence interval to estimate the average number of flights per day handled by the system...
A national air traffic control system handled an average of 47 comma 779 flights during 29...
A national air traffic control system handled an average of 47 comma 779 flights during 29 randomly selected days in a recent year. The standard deviation for this sample is 6 comma 218 flights per day. Complete parts a through c below. a. Construct a 99 ​% confidence interval to estimate the average number of flights per day handled by the system. The 99 ​% confidence interval to estimate the average number of flights per day handled by the system...
Pacific Brant ~ Air traffic affects the migratory flights of a species of small goose called...
Pacific Brant ~ Air traffic affects the migratory flights of a species of small goose called the Pacific Brant. When an aircraft flies over a flock of birds, it is called overflight. To estimate the proportion of overflights that affect Pacific Brant’s migratory flights, Wayne takes a random sample of 494 overflights and finds that 349 of them affected Pacific Brant’s migratory flights. Using this data, Wayne wants to estimate the actual proportion of Pacific Brant’s migratory flights that are...
The traffic control system inside Riyadh city is not meeting the expectations of the city traffic...
The traffic control system inside Riyadh city is not meeting the expectations of the city traffic police. The system is to be updated within a few weeks to incorporate the traffic intensity, the weather conditions and the VIP movements etc. The entire project is to be completed within 10 weeks as per the following schedule: Task ID Task Allocated Time (Weeks) Budget (SAR) TID-10 Requirements elicitation 1 10,000 TID-11 Use-case Development 1 10,000 TID-12 Process Model Development 1 10,000 TID-13...
The Federal Aviation Administration is a government agency that is in charge of air traffic control....
The Federal Aviation Administration is a government agency that is in charge of air traffic control. All of the capital equipment (radar, etc.) used by air traffic controllers is purchased through appropriations from Congress. When Apple Corporation purchases new capital equipment, the decision is made by owners and managers that believe the firm can get a return on investment from the new capital because the new capital can be used to produce new and improved goods for Apple customers. Which...
The Federal Aviation Administration is a government agency that is in charge of air traffic control....
The Federal Aviation Administration is a government agency that is in charge of air traffic control. All of the capital equipment (radar, etc.) used by air traffic controllers is purchased through appropriations from Congress. When Apple Corporation purchases new capital equipment, the decision is made by owners and managers that believe the firm can get a return on investment from the new capital because the new capital can be used to produce new and improved goods for Apple customers. Which...
1. A scientist is interested in whether the design of an air traffic control display affects...
1. A scientist is interested in whether the design of an air traffic control display affects how many airplanes an air traffic controller can manage at once. The scientist evaluates 2 different displays: A low information display (airplanes shown as uniform blips) and a high information display (airplanes shown as different blips depending on aircraft model, and color coded according to speed). The scientist recruits 20 air traffic controllers and randomly assigns 10 to each display condition. The researcher asks,...
It is a calm summer day in southeast Iowa at the Ottumwa air traffic control radar...
It is a calm summer day in southeast Iowa at the Ottumwa air traffic control radar installation - except there are some small, locally intense thunderstorms passing through the general area. Only two planes are in the vicinity of the station: American Flight 1003 is traveling from Minneapolis to New Orleans is approaching from the north-northwest, and United Flight 336 is traveling from Los Angeles to New York is approaching from west-southwest. Both are on the path that will take...
ADVERTISEMENT
Subjects
ADVERTISEMENT
Latest Questions
ADVERTISEMENT