Question

Listed below are systolic blood pressure measurements​ (in mm​ Hg) obtained from the same woman. Find the regression​ equation, letting the right arm blood pressure be the predictor​ (x) variable. Find the best predicted systolic blood pressure in the left arm given that the systolic blood pressure in the right arm is 90 mm Hg. Use a significance level of 0.05.

Right Arm	102	101	93	78	78
Left Arm	176	169	143	145	144

A) The regression equation is y = ____+____x

B) Given that the systolic blood pressure in the right arm is 90 mm Hg, the best predicted systolic blood pressure in the left arm is _____ mm Hg.

Answer 1

Solution:

From given data , we prepare a table.

X	Y	XY	X^2	Y^2
102	176	17952	10404	30976
101	169	17069	10201	28561
93	143	13299	8649	20449
78	145	11310	6084	21025

n	4
sum(XY)	59630.00
sum(X)	374.00
sum(Y)	633.00
sum(X^2)	35338.00
sum(Y^2)	101011.00
Numerator	1778.00
Denominator	2225.30
r	0.7990
r square	0.6384
Xbar(mean)	93.5000
Ybar(mean)	158.2500
SD(X)	9.6047
SD(Y)	14.4806
b	1.2046
a	45.6192

A) Slope of the regression line is

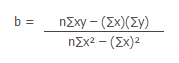
   b = 1.2046

Now , y intercept of the line is

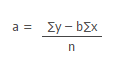
   a = 45.6192

The equation of the regression line is

= a + bx

Answer : = 45.6192 + 1.2046x

B) For x = 90 , find the predicted value of y .

Put x = 90 in the regression line equation.

= a + bx

= 45.6192 + (1.2046 * 90)

  = 154.0332