Question
In: Physics
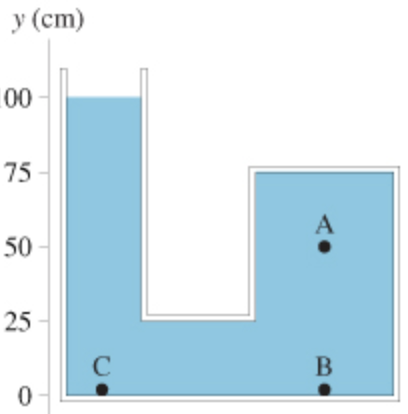
the container shown in (figure 1) is filled with oil. it is open to the atmosphere on the left.
The container shown in (figure 1) is filled with oil. It is open to the atmosphere on the left.
Solutions
Expert Solution
Concepts and reason
The concept used to solve this problem is pressure in fluid. First find the pressure at point A by subtracting the final height and height at the point A. Again, find the pressure difference between the points \(\mathrm{A}\) and \(\mathrm{B}\) by subtracting the height at point \(\mathrm{A}\) and height at point \(B\). Finally, find the pressure difference between the points \(\mathrm{A}\) and \(\mathrm{C}\) by subtracting the height at point \(\mathrm{A}\) and height at point \(C\)
Fundamentals
The pressure is defined as the force divided by per unit area. Here, the oil is filled in a partially closed container. A force applied in one area can result in a greater force in another area. Due to the force of gravity the pressure exerted by a fluid at equilibrium at a given point within the fluid, is called hydrostatic pressure. The expression for the liquid pressure is, \(p=\rho g h\)
Here, \(p\) is the pressure, \(\rho\) is the density of the oil, \(g\) is the gravitational constant, and \(h\) is the height.
(1) The expression for the liquid pressure is, \(p=\rho g h \ldots \ldots\)
Here the height of the pressure for point \(\mathrm{A}\) is, The expression for the height of the pressure is, \(h=h_{f}-h_{i}\)
Here, \(h\) is the height of the pressure, \(h_{f}\) is the final height and \(h_{i}\) is the height at the point \(\mathrm{A}\). From the diagram the final height is \(100 \mathrm{cmand}\) the height at the point \(\mathrm{A}\) is \(50 \mathrm{~cm}\).
$$ \begin{array}{c} h=100 \mathrm{~cm}\left(\frac{1 \mathrm{~m}}{10^{2} \mathrm{~cm}}\right)-50 \mathrm{~cm}\left(\frac{1 \mathrm{~m}}{10^{2} \mathrm{~cm}}\right) \\ =100 \times 10^{-2} \mathrm{~m}-50 \times 10^{-2} \mathrm{~m} \\ =0.5 \mathrm{~m} \end{array} $$
Substitute \(900 \mathrm{~kg} / \mathrm{m}^{3}\) for \(\rho, 9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) and \(0.5 \mathrm{~m}\) for \(h\) in equation (1)
\(p=\left(900 \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)(0.5 \mathrm{~m})\)
$$ =4410 \mathrm{pa}\left(\frac{10^{-3} \mathrm{kpa}}{\mathrm{pa}}\right) $$
\(=4.410 \mathrm{kpa}\)
The absolute pressure \(\mathrm{P}\) is, \(P=P_{0}+p\)
Here, \(P_{0}\) is the atomic pressure. Substitute 4.410 kpa for \(p\) and \(101.325 \mathrm{kPa}\) for \(P_{0}\).
$$ \begin{array}{c} P=101.325 \mathrm{kPa}+4.410 \mathrm{kpa} \\ =105.7 \mathrm{kPa} \end{array} $$
Part 1 The pressure at the point \(\mathrm{A}\) is \(105.7 \mathrm{kPa}\).
The Pressure of a liquid depends on the density of the liquid, acceleration due to gravity, and the distance. This can be viewed from the expression of the pressure: \(p=\rho g h\).
(2) The expression for the liquid pressure is, \(p=\rho g h \ldots \ldots(1)\)
Here the height of the pressure difference between the point \(\mathrm{A}\) and \(\mathrm{B}\) is, The expression for the height of the pressure is, \(h=h_{A}-h_{B}\)
Here, \(h_{A}\) is the height at the point \(\mathrm{A}\) and \(h_{B}\) is the height at the point \(\mathrm{B}\). From the diagram the height at the point Ais \(50 \mathrm{cmand}\) the height at the point \(\mathrm{B}\) is \(0 \mathrm{~cm}\).
$$ \begin{array}{c} h=50 \mathrm{~cm}\left(\frac{1 \mathrm{~m}}{10^{2} \mathrm{~cm}}\right)-0 \mathrm{~cm} \\ =50 \times 10^{-2} \mathrm{~m} \\ =0.5 \mathrm{~m} \end{array} $$
Substitute \(900 \mathrm{~kg} / \mathrm{m}^{3}\) for \(\rho, 9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) and \(0.5 \mathrm{~m}\) for \(h\) in equation (1)
$$ \begin{array}{c} p=\left(900 \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)(0.5 \mathrm{~m}) \\ =4410 \mathrm{pa} \\ =4.410 \mathrm{kpa} \end{array} $$
Part 2 The pressure difference between the points \(\mathrm{A}\) and \(\mathrm{B}\) is \(4.410 \mathrm{kpa}\).
The atmospheric pressure that acts on the surface of a liquid is the total pressure acting on a liquid. The Pressure of a liquid depends on the density of the liquid, acceleration due to gravity, and the distance.
(3) The expression for the liquid pressure is, \(p=\rho g h \ldots \ldots(1)\)
Here the height of the pressure difference between the point \(\mathrm{A}\) and \(\mathrm{C}\) is, The expression for the height of the pressure is, \(h=h_{A}-h_{C}\)
Here, \(h_{A}\) is the height at the point \(\mathrm{A}\) and \(h_{C}\) is the height at the point \(\mathrm{C}\). From the diagram the height at the point \(\mathrm{A}\) is \(50 \mathrm{cmand}\) the height at the point \(\mathrm{C}\) is \(0 \mathrm{~cm}\).
$$ \begin{array}{c} h=50 \mathrm{~cm}\left(\frac{1 \mathrm{~m}}{10^{2} \mathrm{~cm}}\right)-0 \mathrm{~cm} \\ =50 \times 10^{-2} \mathrm{~m} \\ =0.5 \mathrm{~m} \end{array} $$
Substitute \(900 \mathrm{~kg} / \mathrm{m}^{3}\) for \(\rho, 9.8 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) and \(0.5 \mathrm{~m}\) for \(h\) in equation (1)
$$ \begin{array}{c} p=\left(900 \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.8 \mathrm{~m} / \mathrm{s}^{2}\right)(0.5 \mathrm{~m}) \\ =4410 \mathrm{pa} \\ =4.410 \mathrm{kpa} \end{array} $$
Part 3 The pressure difference between the points \(\mathrm{A}\) and \(\mathrm{C}\) is \(4.410 \mathrm{kpa}\).
The pressure won't depend on the amount of liquid present. Pressure is same in all directions of the fluid for given points.
Part 1
The pressure at the point \(\mathrm{A}\) is \(105.7 \mathrm{kPa}\).
Part 2
The pressure difference between the points \(\mathrm{A}\) and \(\mathrm{B}\) is \(4.410 \mathrm{kpa}\).
Part 3
The pressure difference between the points \(A\) and \(C\) is \(4.410 \mathrm{kpa}\).
Related Solutions
A large storage tank, open to the atmosphere at the top and filled with water, develops...
A large storage tank, open to the atmosphere at the top and filled with water, develops...
A large storage tank, open to the atmosphere at the top and filled with water, develops...
A large storage tank, open to the atmosphere at the top and filled with water, develops...
In the figure, the top tank, which is open to the atmosphere, contains water and the...
Water flows steadily from an open tank as shown in the figure. (Figure 1) The elevation...
A “U” shaped tube (with a constant radius) is filled with water and oil as shown....
Water flows steadily from an open tank as shown in the figure
Water flows steadily from an open tank as shown in the figure.
A) For the circuit shown in the figure, find the current throughresistor R1=6.0?(left).B)For the...
- Which of the following redox reactions do you expect to occur spontaneously in the reverse direction?...
- 2(a) A typical metallic particle has a rest mass (i.e. mass when the particle is not...
- In 500 words minimum: Evaluate when dividends are taxable, who they are taxable to, and the...
- 4. How might the researchers approach the measurement of validity? 5. What can the researchers do...
- Quick Answers. ty _____. 27. Environmental scanning is an important activity for an organization, it represents...
- The following tables form a Library database held in an RDBMS: Borrower (card_no , last_name ,...
- Create a html page to convert miles into kilometers, the page should have four buttons using...
 Dr. OWL answered 5 years ago
Dr. OWL answered 5 years ago