Question
In: Physics
Find the moment of inertia Ix of particle a with respect to the x axis
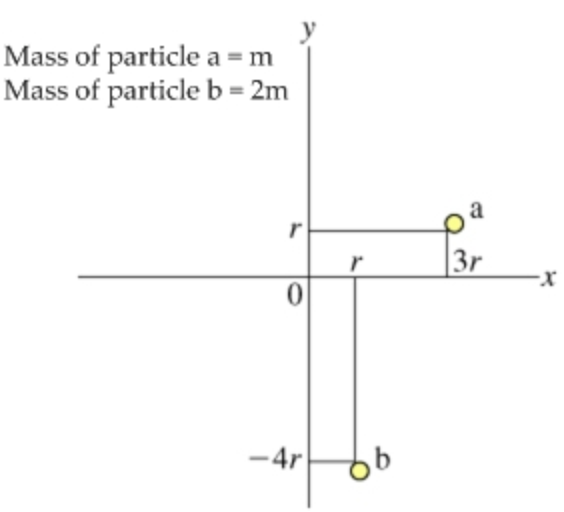
Solutions
Expert Solution
Concepts and reason
The concept required to solve the problem is the moment of inertia. Use the mass and the distance from \(\mathrm{x}\) axis to calculate the moment of inertia with respect to \(\mathrm{x}\) axis. Use the mass and the distance from y axis to calculate the moment of inertia with respect to y axis. Calculate the sum of the moment of inertias with respect to \(\mathrm{x}\) and \(\mathrm{y}\) axis to calculate the moment of inertia with respect to \(\mathrm{z}\) axis.
Fundamentals
The moment of inertia of the object is, \(I=M R^{2}\)
Here, \(M\) is the mass of the object and \(R\) is the perpendicular distance.
(C. 1) The moment of inertia of particle is, \(I=M R^{2}\)
The mass of particle a is \(m\) and the perpendicular distance of particle a from \(\mathrm{x}\) axis is \(r\). Substitute \(m\) for \(M\) and \(r\) for \(R\). The moment of inertia of particle a with respect to \(\mathrm{x}\) axis is, \(I_{x}=m r^{2}\)
Part C.1 The moment of inertia of particle a with respect to \(\mathrm{x}\) axis, \(I_{x},\) is \(\mathrm{mr}^{2}\)
The moment of inertia of the particle a with respect to x axis is the product of mass of particle a and the square of perpendicular distance from \(\mathrm{x}\) axis.
(C. 2) The moment of inertia of particle is, \(I=M R^{2}\)
The mass of particle a is \(m\) and the perpendicular distance of particle a from y axis is \(3 r\). Substitute \(m\) for \(M\) and \(3 r\) for \(R\). The moment of inertia of particle a with respect to y axis is,
$$ I_{y}=m(3 r)^{2} $$
\(=9 m r^{2}\)
Part C.2 The moment of inertia of particle a with respect to \(\mathrm{y}\) axis, \(I_{y},\) is \(9 \mathrm{mr}^{2}\)
The moment of inertia of the particle a with respect to \(\mathrm{y}\) axis is directly proportional to mass of particle \(a\) and the square of perpendicular distance from y axis.
(C.3) The moment of inertia of particle a with respect to \(z\) axis is, \(I_{z}=I_{x}+I_{y}\)
Substitute \(m r^{2}\) for \(I_{x}\) and \(9 m r^{2}\) for \(I_{y}\). The moment of inertia of the particle with respect to \(z\) axis is,
\(I_{z}=m r^{2}+9 m r^{2}\)
$$ =10 m r^{2} $$
Part C.3 The moment of inertia of particle a with respect to \(z\) axis, \(I_{z},\) is \(10 m r^{2}\)
The moment of inertia of the particle a with respect to \(z\) axis is the sum of the moment of inertia of particle a with respect to x axis and the sum of the moment of inertia of particle a with respect to y axis.
Part C.1 The moment of inertia of particle a with respect to \(\mathrm{x}\) axis, \(I_{x},\) is \(\mathrm{mr}^{2}\)
Part \(\mathrm{C} .2\) The moment of inertia of particle a with respect to \(\mathrm{y}\) axis, \(I_{y},\) is \(9 \mathrm{mr}^{2}\)
Part \(C .3\) The moment of inertia of particle a with respect to \(z\) axis, \(I_{z},\) is \(10 m r^{2}\)
Related Solutions
Find the mass, the center of mass, and the moment of inertia about the z-axis for...
We will find the Moment of Inertia Moment and Polar Moment of Inertia of a U...
For the shape shown below, calculate the moment of inertia about the x axis. (Figure 8)The...
Find the moments of inertia Ix, Iy, I0 for a lamina in the shape of an...
Twenty equal measurements of the moment of inertia of the cranked shaft relative to the axis...
To calculate moment of inertia
moment of inertia of a rod
The parallel axis theorem relates Icm, the moment of inertia of an object about an axis passing through its center of m...
A toy top with a spool of diameter 5.0cm has a moment of inertia of 3.0x10^-5kg x m^2 about its rotation axis.
Find the moment of inertia of a circular disk of radius R and mass M that...
- The Drunkard’s (Random) Walk. Imagine you live on an infinite grid of streets where locations are...
- Problem 13-15 The Ashland Company recently hired you to review its control procedures for the purchase,...
- A transformer contains four times as many turns in the secondary coil as it does in...
- The C5H5+ and C5Cl5+ cations, which have never been isolated, are known to be ground state...
- A gymnast of mass 62.0kg hangs from a vertical rope attached to the ceiling. You can...
- Sharp Company manufactures a product for which the following standards have been set: Standard Quantity or...
- (a) In a proton at one certain moment, the down quark has a strong color charge...
 Dr. OWL answered 5 years ago
Dr. OWL answered 5 years ago