Question

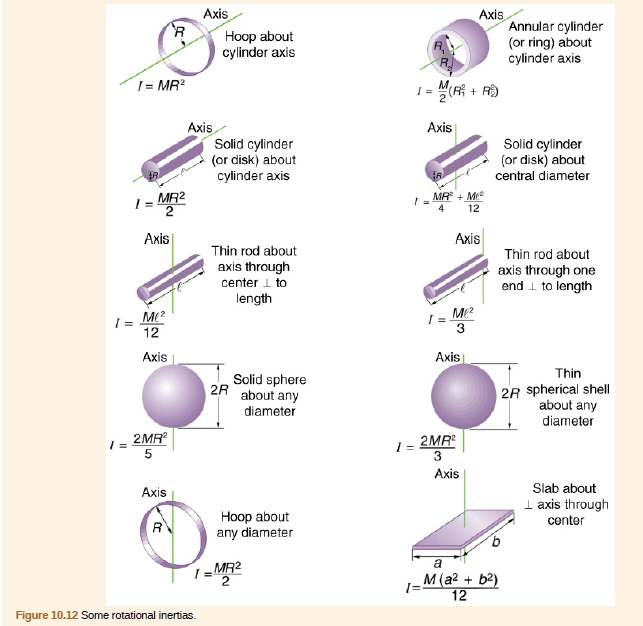
Starting with the formula for the moment of inertia of a rod rotated around an axis through one end perpendicular to its length (I=M ℓ² / 3), prove that the moment of inertia of a rod rotated about an axis through its center perpendicular to its length is I=M ℓ² / 12. You will find the graphics in Figure 10.12 useful in visualizing these rotations.

 

Answer 1

 

A moment of inertia represents the body's tendency to resist rotational motion. It is given by the product of mass and square of the distance from the axis of rotation.

I=M R²

The parallel axis theorem states that: the moment of inertia increases when the axis of rotation moves away. It is the sum of moment of inertia through the center of mass and product of group and square of perpendicular distance from the rotation axis and center of the assembly.

I=Ic m+M d²

We know that when the rod rotates about a parallel axis passing through the end of the rod, the moment of inertia is:

I=1/3 M l²

Where M is the mass of the rod and l is the length of the rod.

The distance from the end of the rod to the center is d=l/2.

 

I=Ic m+M d² 

=> Icm=I-M d²

 

Therefore:

Icm =1/3 Ml²-M(l/2)² 

Icm =1/3 Ml²-1/4 Ml² 

Icm =1/12 Ml²

 

 

Hence proved that moment of inertia of the rod about the axis passing through its center of mass and perpendicular to it is Ml²/12