Question

For each of the actions depicted below, a magnet and/or metal loop moves with velocity v? (v? is constant and has the same magnitude in all parts). Determine whether a current is induced in the metal loop. If so, indicate the direction of the current in the loop, either clockwise or counterclockwise when seen from the right of the loop. The axis of the magnet is lined up with the center of the loop.

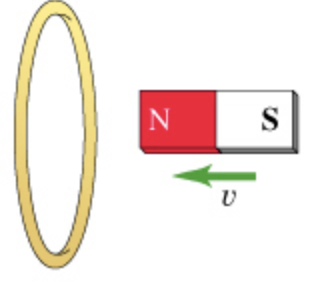
Part A

For the action depicted in the figure, (Figure 1) indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop).

• a.) clockwise
• b.) counterclockwise
• c.) zero

 

Part B

For the action depicted in the figure, (Figure 2) indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop).

• a.) clockwise
• b.) counterclockwise
• c.) zero

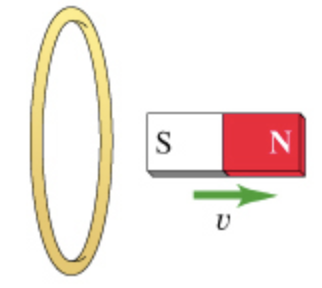
Part C

For the action depicted in the figure, (Figure 3) indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop).

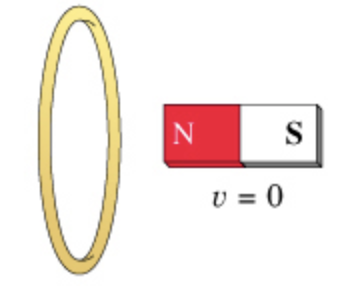
• a.) clockwise
• b.) counterclockwise
• c.) zero

 

Part D

For the action depicted in the figure, (Figure 4) indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop).

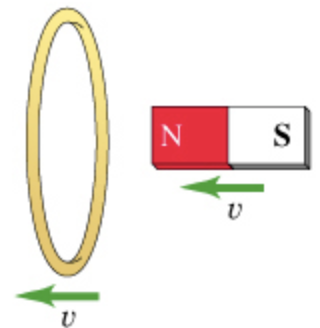
• a.) clockwise
• b.) counterclockwise
• c.) zero

 

Part E

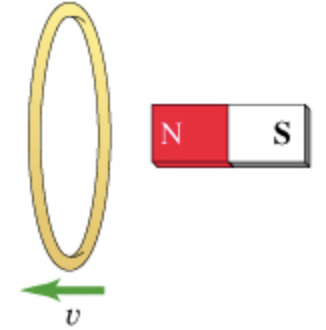
For the action depicted in the figure, (Figure 5) indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop).

• a.) clockwise
• b.) counterclockwise
• c.) zero

Answer 1

Concepts and reason

The concept of Lenz's law is used here. First out how the flux linking to the coil changes. If the flux linking to the coil increases, then the induced current points in such direction that opposes the increase of the flux and vice-versa. Apply that information in all the parts and find out the direction of induced current.

Fundamentals

Lenz's law is based on the Faraday's law of electromagnetic induction. The Faraday's law of electromagnetic induction states that when the magnetic field in a coil changes, emf is induced in the coil. The magnetic field change is caused by moving a magnet towards or away from the coil. In other words, the emf induced in a coil depends on the rate of change of flux. Lenz's law states that the induced emf in a coil generates current in such a way that opposes the increase in the magnetic flux.

 

(A) When the north pole of the magnet moves towards the coil, the magnetic flux linking to the coil increases. This magnetic flux change induces emf in the coil according to the Faraday's law. This induced emf produces current in the coil in such a way that oppose the increases in flux value. To oppose that increase, the face of the coil towards the north pole of the magnet becomes a north pole which produces force of repulsion between them. This force of repulsion opposes the motion of magnet. Hence, the direction of the inducted current will be counter clockwise as seen from the magnet. \([\) Part \(A]\)

Part A The direction of the inducted current in the loop is counter clockwise.

As we know the like poles repel each other and unlike poles attract each other. To oppose the motion of the magnet, repulsion produces between magnet and coil and this occurs when the face of the coil becomes North pole.

 

(B) When the north pole of the magnet moves away the coil, the magnetic flux linking to the coil decreases. This magnetic flux change induces emf in the coil according to the Faraday's law. This induced emf produces current in the coil in such a way that oppose the decrease in flux value. To oppose that decrease, the face of the coil towards the south pole of the magnet becomes a north pole which produces force of attraction between them. This force of attraction opposes the motion of magnet. Hence, the direction of the inducted current will be counter clockwise as seen from the magnet. \([\) Part B \(]\)

Part B The direction of the inducted current in the loop is counter clockwise.

As we know the like poles repel each other and unlike poles attract each other. To oppose the motion of the magnet, attraction produces between magnet and coil and this occurs when the face of the coil becomes North pole. The coil with the North pole producing current in counter clockwise direction.

 

(C) The magnet is stationary in this case. Hence, there is no change occurs in the magnetic flux value linked with the coil which implies that the no emf is induced in the coil and no induced current flows in the coil. \([\) Part \(C]\)

Part \(C\) The inducted current in the loop is zero.

The stationary magnet implies no induced emf and no current is induced in the coil.

 

(D) The magnet and coil both moves with the same velocity which implies that the magnet is not getting closer or farther away from the coil. This implies that no change in flux value occurs in the coil. Hence, there is no change occurs in the magnetic flux value linked with the coil which implies that the no emf is induced in the coil and no induced current flows in the coil. \([\) Part D \(]\)

Part D

The inducted current in the loop is zero.

since, the magnet and coil both moves with the same velocity which implies that the magnet is not getting closer or farther away from the coil. Hence, there is no emf is induced in the coil and no induced current generates in the coil.

 

(E) When the coil moves away the from, the magnetic flux linking to the coil decreases. This magnetic flux change induces emf in the coil according to the Faraday's law. This induced emf produces current in the coil in such a way that oppose the decrease in flux value. To oppose that decrease, the face of the coil towards the north pole of the magnet becomes a south pole which produces force of attraction between them. This force of attraction opposes the motion of magnet. Hence, the direction of the inducted current will be clockwise as seen from the magnet. [Part E]

Part \(E\) The direction of the inducted current in the loop is clockwise.

As we know the like poles repel each other and unlike poles attract each other. To oppose the motion of the magnet, attraction produces between magnet and coil and this occurs when the face of the coil becomes south pole. The coil with the south pole producing current in the clockwise direction.