Question

A phase transition from solid to liquid takes place at constant pressure and temperature. This is a closed PVT system. (a) Show that the Gibbs free energy G = U - TS + PV is a constant. (b) The solid and liquid phases are in equilibrium at a temperature T and pressure P, where G(solid) = G(solid)(T,P) and G(liquid) = G(liquid)(T,P). The phases are also in equilibrium at the neighboring temperature T +dT and pressure P + dP, where G(solid) = G(solid)(T+dT, P+dP) and G(liquid) = G(liquid)(T+dT, P+dP). Show that at temperature T, (dP/dT) = (S(liquid) - S(solid)) / (V(liquid) - V(solid)) where S and V denote entropy and volume respectively.

Answer 1

Free energy, in thermodynamics, energy-like property or state function of a system in thermodynamic equilibrium. Free energy has the dimensions of energy, and its value is determined by the state of the system and not by its history. Free energy is used to determine how systems change and how much work they can produce. It is expressed in two forms: the Helmholtz free energy F, sometimes called the work function, and the Gibbs free energy G. If U is the internal energy of a system, PV the pressure-volume product, and TS the temperature-entropy product (T being the temperature above absolute zero), then F = U − TS and G = U + PV − TS. The latter equation can also be written in the formG = H – TS, where H = U + PV is the enthalpy. Free energy is an extensive property, meaning that its magnitude depends on the amount of a substance in a given thermodynamic state.

The Gibbs free energy total differential natural variables may be derived via Legendre transforms of the internal energy.

.

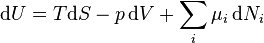Because S, V, and N_i are extensive variables, Euler's homogeneous function theorem allows easy integration of dU

.

The definition of G from above is

.

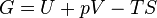Taking the total differential, we have

.

Replacing dU with the result from the first law gives

.

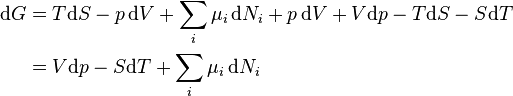The natural variables of G are then p, T, and {N_i}.