Question

In: Economics

A consumer has an income of $1,000 to spend on food and medicine. The price of...

A consumer has an income of $1,000 to spend on food and medicine. The price of one unit of food is $$5 and the price of one unit of medicine is $10. For each question, write down the mathematical expression of the budget constraint and draw it carefully. Put food on the x-axis and medicine on the y-axis. Label the intercepts, slopes, and kinks.

Suppose the consumer receives coupons for 50 units of food and those can only be used to buy food.
Suppose the consumer receives coupons for 50 units of food and can sell the coupons at half of the market price of the food.
Instead of the coupon, the consumer receives a 10% discount for additional units of food that exceed 100 units. That is, the consumer pays $5 for each of the first 100 units and $4.5 for each additional unit.

Expert Solution

A budget constraint shows the various combinations of two goods ,a consumer can afford to buy.

Let X be the units of food , Y be the units of medicine and M be the budget or income of the consumer.

Budget constraint ( mathematical expression)----------

M= 5X+10Y

X. Y

200. 0

0. 100

Diagramatic expression of budget line-----

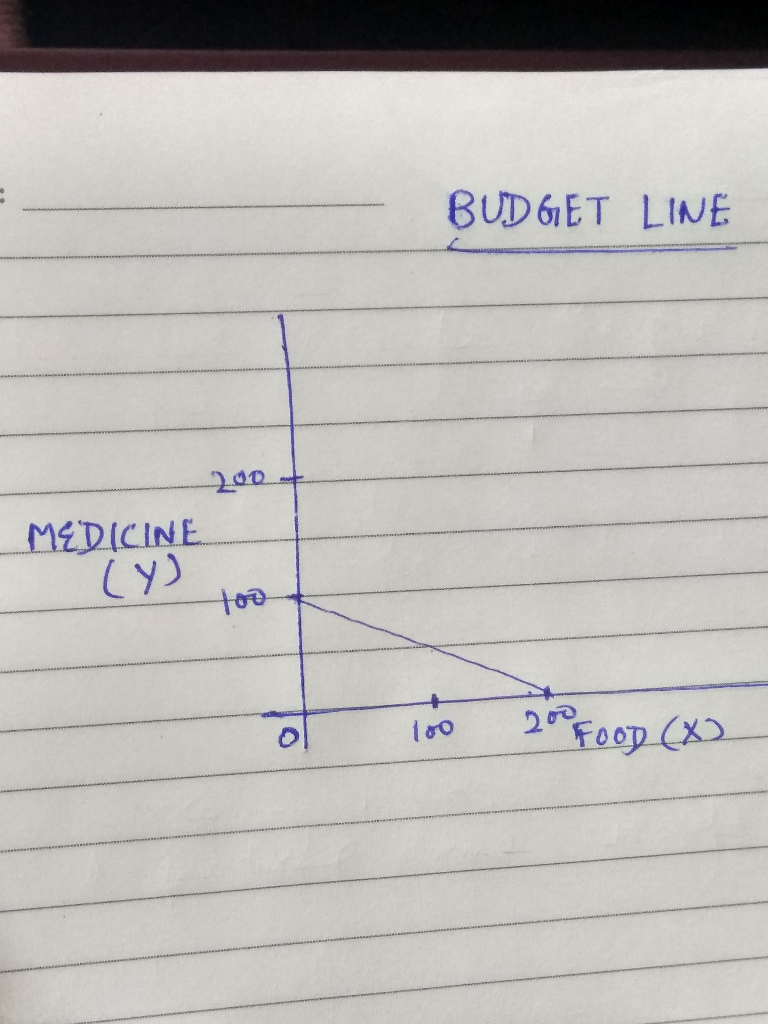
Intercept of budget line-----

Horizontal intercept( X) is the point----- 200,0

Vertical intercept (Y) is the point --------0,100

Slope of budget line-------

slope of budget line is the rate of change.It is the price of X in terms of Y

Px/ Py= Qy/Qx

5/10 or 100/200

= 1/2

#When consumer received 50 units of food coupons------

Horizontal intercept(X)----250,0

Vertical intercept(Y)-------0,100

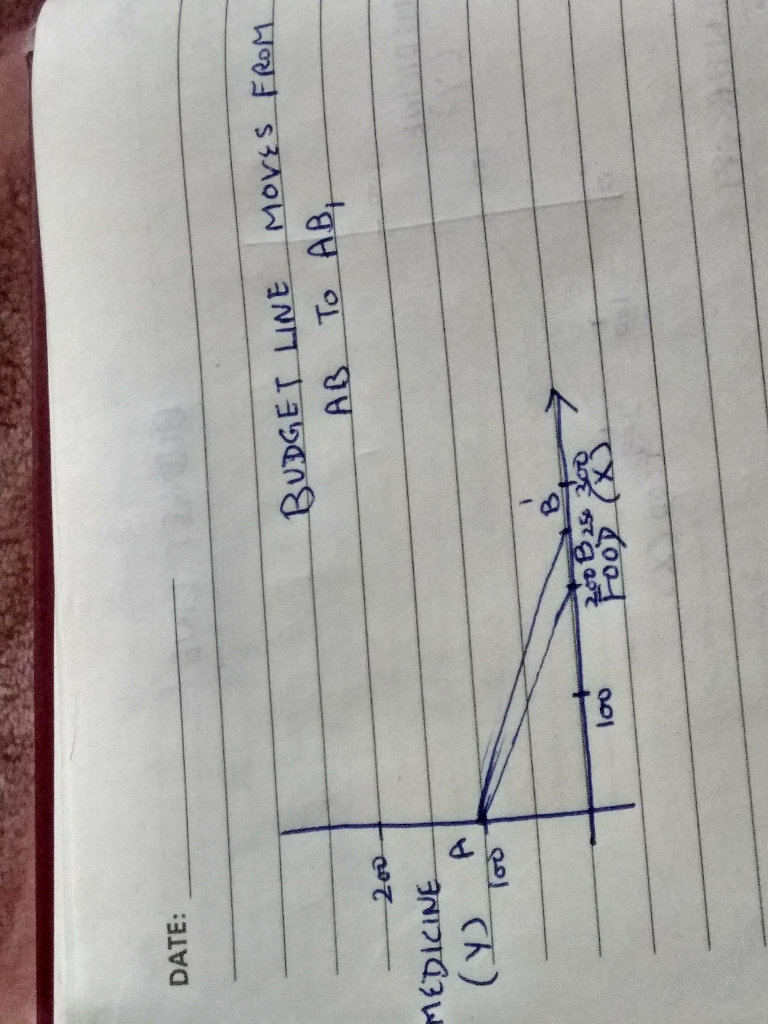
Slope of budget line in terms of quantity--

Qy/ Qx

100/250

2/5

Kink of budget line is the movement from B to B'

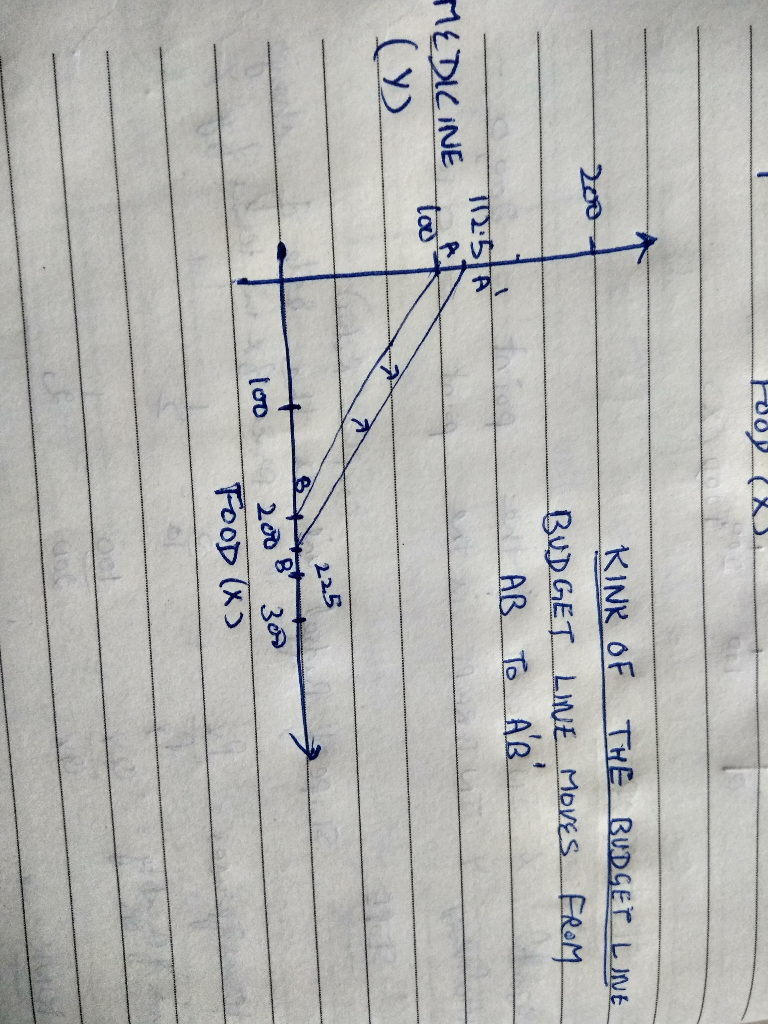
when 50 units food coupons are sold half the market price of coupons----

Intercept ( horizontal) X-----225 , 0

Intercept ( vertical)Y---------0 ,112•5

As his real income to spend has increased from $1000 to $1125

Slope of budget line --- Qy/Qx

1125/225

45/9

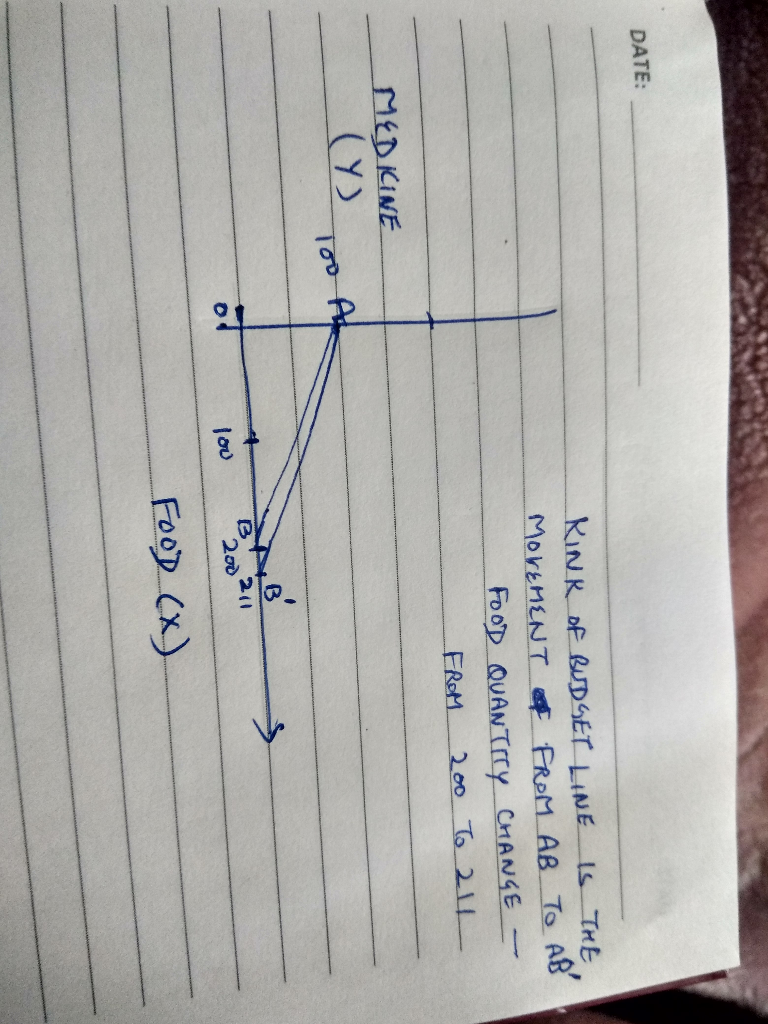
If he pays $5 for first 100 units &$4•5 for additional units of food-------

food ( X) intercept = 211,0

Medicine Y intercept =0,100

Slope of budget line -----

Qy/Qx-----100/211

Rahul Sunny answered 4 hours ago

An individual consumer has an income of $100 to spend on twogoods, which are food...

An individual consumer has an income of $100 to spend on two goods, which are food and clothes. When each of these two goods has a price of $2 per unit, the individual spends equal amounts on food and clothes.(a) For the above set of income and prices, illustrate the consumer's equilibrium diagrammatically, showing the budget line and indifference curves.(b) If the government then provides the individual with a subsidy of $1 for every unit of food purchased, how many...

A consumer spends all her income on food and clothing. At the current prices, the price...

A consumer spends all her income on food and clothing. At the current prices, the price of food is K10 and the price of clothing is K5, she maximizes her utility by purchasing 20 units of food and 50 units of clothing.(a) What is the consumer’s income? What is the consumer’s MRS of food for clothing at the equilibrium position?

you have $100 to spend on food and clothing. the price of food is $4, and...

you have $100 to spend on food and clothing. the price of food is $4, and the price of clothing is $10. A. graph your budget constraint B. suppose the government subsidizes clothing such that each unit of clothing is half price, up yo the first five units of clothing. Graph your budget constraint in this circumstance.

has the pandemic and income allowed consumers to spend more at resturants and the food industry?

Since 1960, the percent of disposable income that Americans spend on food has declined to about...

Since 1960, the percent of disposable income that Americans spend on food has declined to about 10% from approximately 17%. That change represents a significant increase in the “affordability” of food since it now represents a much smaller portion of spending. List and explain two reasons why the true impact on American food purchasing is even more significant than the decline in percent spent on food indicates.

If we know that Bridget is a consumer who does not spend all of her income,...

If we know that Bridget is a consumer who does not spend all of her income, what else can we deduce? a. Her budget line has moved outwards. b. Her budget line has moved inwards. c. She is operating at a point outside her budget line. d. She is operating at a point inside her budget line. Opportunity cost ______ directly involved in consumer choice; production costs ______ directly involved in consumer choice. a. is; are b. is; are not...

Suppose that I have an income of $240 to spend on cat food (good x) and...

Suppose that I have an income of $240 to spend on cat food (good x) and cat toys (good y). The price of food is $30 per bag and the price of toys are $10 each. My utility function is given as U(x,y)=xy a) Solve my optimization problem. What is the optimal amount of food and toys that I should buy? b) Suppose I can get a Costco membership for $60 and I can buy cat food for $20 per...

A consumer has an income of $120 to buy two goods (X, Y). the price of...

A consumer has an income of $120 to buy two goods (X, Y). the price of X is $2 and the price of Y is $4. The consumer utility function is given by UX,Y=X2/3*Y1/3 You are also told that his marginal utilities are MUX=23YX1/3 MUY=13XY2/3 Find the slope of the budget constrain. (1 point) Calculate the optimal quantity of good X and Y for this consumer (Point A). (2 points) Assume that the price of good X...

A consumer group wished to compare the price of food items at two supermarkets A and...

A consumer group wished to compare the price of food items at two supermarkets A and B. A random sample of 8 items was selected and the cost of the items at each supermarket was recorded on a particular day. Item 1 2 3 4 5 6 7 8 A $3.60 $3.73 $3.48 $2.43 $2.81 $2.66 $3.62 $2.40 B $3.38 $3.77 $3.50 $2.55 $2.82 $2.65 $3.74 $2.31 (a) test at α = .05 if "on average" the prices offered at...

Jane’s current income is $200, the price of food is $4 and the price of all...

Jane’s current income is $200, the price of food is $4 and the price of all other goods is $1. The government gives Jane $100 in food stamps. Draw her budget line. Draw a set of indifference curves that show that Jane would not care whether she receives $100 in cash or $100 in food stamps. Now a black market developes where Jane can trade $1 of food stamps for $.50 in cash. Draw Jane’s new budget line. Will she...