Question

Billy’s Bakery bakes fresh bagels each morning. The daily demand for bagels is a random variable

with a distribution estimated from prior experience given by

# of Bagels Sold	Probability
0	0.05
5	0.10
10	0.10
15	0.20
20	0.25
25	0.15
30	0.10
35	0.05

The bagels cost Billy’s $0.08 to make, and they are sold for $0.35 each. Bagels unsold at the end

of the day are purchased by a nearby charity soup kitchen for $0.03 each.

a) Simulate the discrete distribution for demand for 100 days, and compare the expected daily profit of Q = 25 and Q = 27.

b) Repeat part a) using a normal distribution with m = 18 and s = 8.86 for demand.

Submit a brief description of how you set up your simulations. This description must explain how you generated the random demands and any formulas that you used.

Answer 1

(a)

c₀ = .08 - .03 = .05

c_u = .35 - .08 = .27

Critical ratio = 0.27/(0.5+0.27) = .84375

From the given distribution, we have:

                Q       f(Q)        F(Q)

                 0        .05         .05

                 5        .10         .15

                10        .10         .25

                15        .20         .45

                20        .25         .70

                                        < - - - - .84375

                25         .15        .85

                30         .10        .95

                35         .05       1.00

Since the critical ratio falls between 25  and 27 the optimal is Q = 25 bagels.

(b) .

     m = 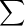xf(x) = (0)(.05) + (5)(.10) +...+(35)(.05) = 18

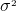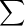     = x^2f(x) - 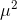= 402.5- 18^2 =78.5

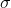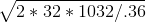   = =8.86

The z value corresponding to a critical ratio of .84375 is 1.01. Hence,

Q* = 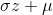= (8.86)(1.01) + 18 = 26.95 ~ 27

ANSWERED

THIS IS 100% CORRECT ANSWER

SO PLEASE RATE ME POSITIVE

THANKS