Question

A random sample of 15 items is drawn from a population whose standard deviation is unknown. The sample mean is x⎯⎯x¯ = 760 and the sample standard deviation is s = 20. Use Appendix D to find the values of Student’s t.

(a)	Construct an interval estimate of μ with 99% confidence. (Round your answers to 3 decimal places.)

The 99% confidence interval is from  to

(b)	Construct an interval estimate of μ with 99% confidence, assuming that s = 40. (Round your answers to 3 decimal places.)

The 99% confidence interval is from  to

(c)	Construct an interval estimate of μ with 99% confidence, assuming that s = 80. (Round your answers to 3 decimal places.)

The 99% confidence interval is from  to

(d)	Describe how the confidence interval changes as s increases.
	The interval stays the same as s increases. The interval gets wider as s increases. The interval gets narrower as s increases

Answer 1

z score for 99% confidence interval is 2.576 (using z distribution table for two tailed test)

(A) The formula for the confidence interval is given as

CI =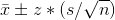

where we have 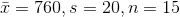and z = 2.576

setting the given values, we get

CI =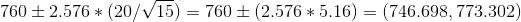

Confidence interval length = upper level - lower limit = 773.302-746.698 = 26.604

(B)

The formula for the confidence interval is given as

CI =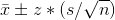

where we have 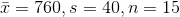and z = 2.576

setting the given values, we get

CI =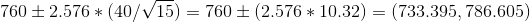

Confidence interval length = upper level - lower limit = 786.605-733.395 = 53.21

(C)

The formula for the confidence interval is given as

CI =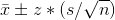

where we have 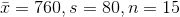and z = 2.576

setting the given values, we get

CI =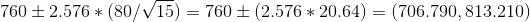

Confidence interval length = upper level - lower limit = 813.210-706.79 = 106.42

(d) It is clear that the confidence interval length is increasing with increase in s value, so we can say that as we increase s value, the confidence interval gets wider.

option B is correct answer