Question

Consider the following CFG with starting variable S and Σ = {1, 2, 3, 4, 5, 6, 7,

8, 9, 0}:

S → X Y Z

X → 1 | 2

Y → W | ε

Z → Z Z | W

W → 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0

a. [20 marks] Create a derivation tree for your student number. - 84521004

b. [20 marks] Is this grammar ambiguous or unambiguous? Briefly explain (Remember the string is 84521004)

why.

Answer 1

a) In the given grammar, there is only one production rule involving S, the rule is S -> XYZ,

With this production rule when we expand X, we can only have 1 or 2 as the first digit.

So This grammar can only produce numbers that begin with either 1 or 2.

We cannot derive string  84521004 using this grammar, since, we cannot produce 8 as the first digit with this grammar.

So, there will be no derivation tree for 84521004.

b) Yes, this grammar is ambiguous.

A grammar is ambiguous if we can generate more than one derivation tree for any string.

Let us take a string 123

We can generate two derivation trees for the same string using this grammar.

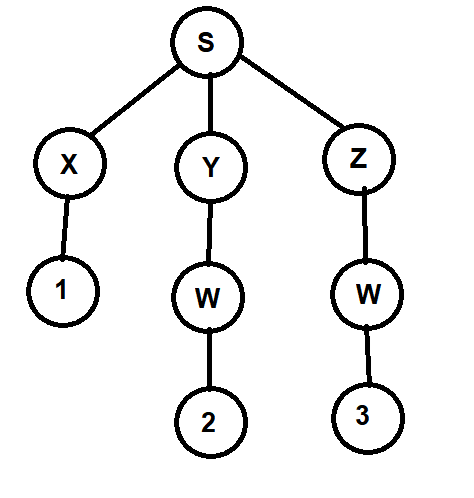
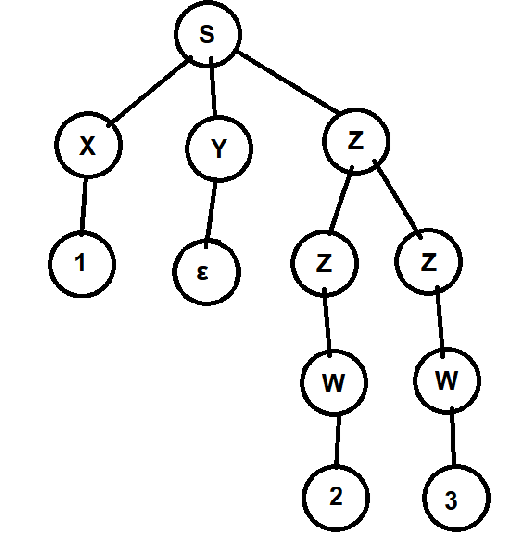
Since we can generate more than one derivation tree using this grammar, this grammar is ambiguous.

------------------------------------------------

UPDATE:

for string 2180045

There are multiple derivation trees possible, one such derivation is below:

-----------------------------------------------

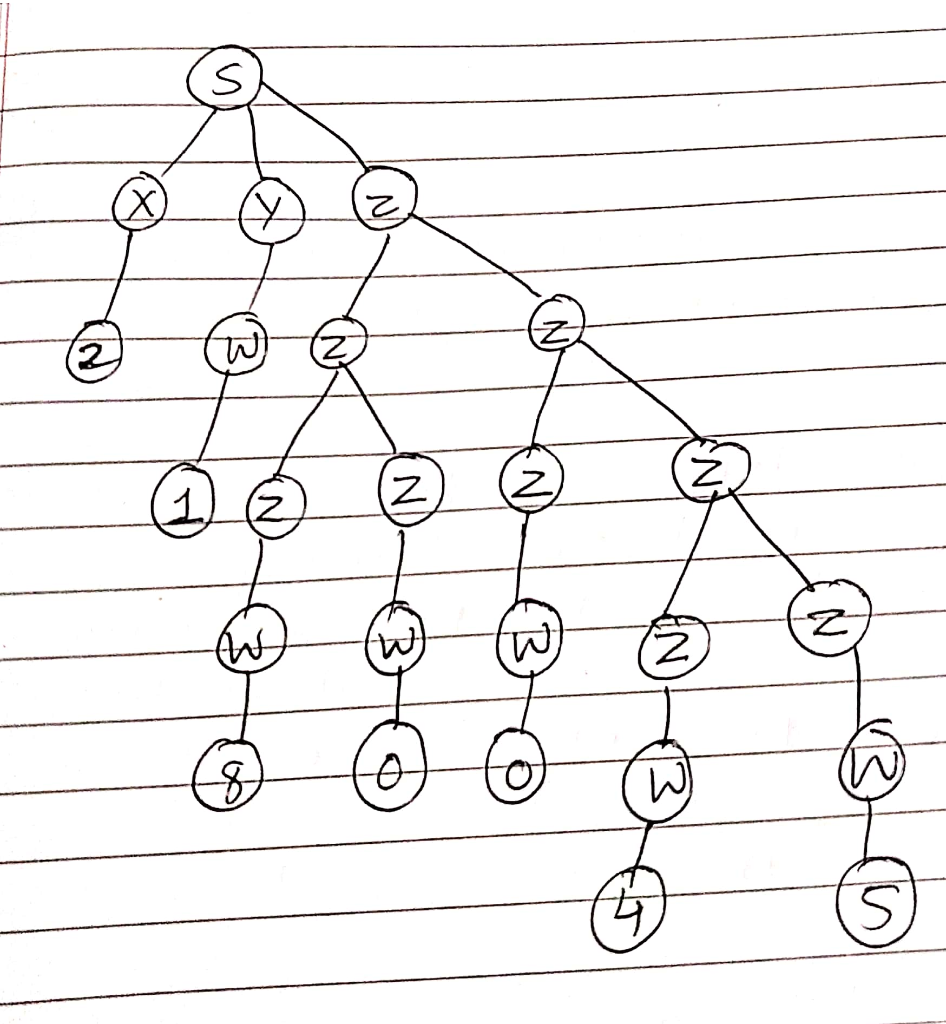
I hope this helps you,

Please rate this answer if it helped you,

Thanks for the opportunity