Question
In: Statistics and Probability
Western Technical Services is a small engineering firm in Colorado that provides a variety of technical...
Western Technical Services is a small engineering firm in Colorado that provides a variety of technical and drafting services. Western Technical Services employs three engineers, five drafters, and three secretaries. Western has developed a leading reputation in the design of low-capacity and medium-capacity heat exchangers for electrical equipment. A large backlog of jobs has accumulated, and the firm has decided it must complete the back orders. The firm wants to maximize the number of jobs finished each day to eliminate its backlog. The average time required to design a medium-capacity heat exchangers is 4 hours of engineering time, 3 hours of time by a drafter, and 3 hours of secretarial work. Designing a low-capacity heat exchanger requires an average of 1.5 hours of work from an engineer, 4 hours of work from a drafter, and 1.5 hours of secretarial effort.
Formulate a linear programming problem that Western could use to determine how best to employ its resources in order to maximize the total number of heat exchangers that can be completed each day subject to the firm’s labor constraints. I.e. the objective of the firm in this problem is to maximized total output (Q). (Hint: Q = 1M + 1L where M = the number of medium capacity heat exchangers completed and L = the number of low capacity heat exchangers completed each day) Assume that the engineers and drafters each work 10-hour days, and the secretaries work 8 hours per day.
Solve the linear programming problem and interpret the solution. How many heat exchangers will be completed each day? Your assignment is to maximize output (i.e. maximize the number total number of heat exchangers produced subject to the constraints provided.) Hint: The total number, i.e. quantity, of heat exchangers is Total output Q = 1M + 1L. You are trying to determine the maximum number the firm can produce given its production constraints.
Solutions
Expert Solution
Let M be the number of medium capacity heat exchangers completed each day and L be the number of low capacity heat exchangers completed per day
these are the decision variables
The total number of heat exhangers produced per day is M+L
The firm wants to maximize the total number of exchangers produced per day
The objective function is to maximize M+L
Following are the constraints
Engineering hours
- Each of the 3 engineers can work 10 hours per day, for a total
30 hours of Engineering time per day. The engineering time required
to produce M and L quantities is
 and this has to be less than or equal to 30
and this has to be less than or equal to 30
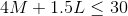
Drafter hours
- Each of the 5 drafters can work 10 hours per day, for a total
50 hours of drafter time per day. The drafter time required to
produce M and L quantities is
 and this has to be less than or equal to 50
and this has to be less than or equal to 50
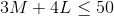
Secretarial hours
- Each of the 3 secretaries can work 8 hours per day, for a total
24 hours of secretarial time per day. The secretarial time required
to produce M and L quantities is
 and this has to be less than or equal to 24
and this has to be less than or equal to 24
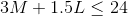
The linear programming model is
maximize

s.t.
We prepare the following excel

get these values

set up the solver using data--->solver

get the following solution

To maximize the total number of exhanges produced per day, given the production constraints, the firm needs to produce 2.8 medium capacity and 10.4 low capacity heat exhangers. The fractional values will indicate the partially completed heat exhangers during the day.
Related Solutions
Part A MelSwin is an accounting consultancy firm that provides its services to small, medium and...
Part A MelSwin is an accounting consultancy firm that provides its services to small, medium and...
Part A MelSwin is an accounting consultancy firm that provides its services to small, medium and...
Part A MelSwin is an accounting consultancy firm that provides its services to small, medium and...
Eclipse Engineering provides services of structural engineering. They just opened a new branch in Portland, OR....
ERF Enterprises provides comprehensive AV services to institutions in the State of Colorado. Their customers fall...
Texas Building Services provides cleaning services for a variety of clients. The company has two producing...
1. The Westfall Relocation Company, located in Denver, Colorado provides services to laid-off employees of major...
Your company provides a variety of delivery services. Management wants to know the volume of a...
Evans Park Evans Park is a small amusement park that provides a variety of rides for...
- Magnolia Manufacturing makes wing components for large aircraft. Kevin Choi is the production manager, responsible for...
- distinguish between microeconomics and macroeconomics
- Balloons By Sunset (BBS) is considering the purchase of two new hot air balloons so that...
- 1. Sonic ran an ad claiming that it could make thousands of drink combinations. This is...
- On December 31, 2016, Monty Corp. provided you with the following pre-adjustment information regarding its portfolio...
- How does the Central Bank can decrease the interest rates in the economy using monetary policy?
- Which choice below will increase the pH of a 0.2 M H2S solution A) Bubble through...
 and this has to be less than or equal to 30
and this has to be less than or equal to 30
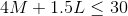
 and this has to be less than or equal to 50
and this has to be less than or equal to 50
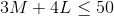
 and this has to be less than or equal to 24
and this has to be less than or equal to 24
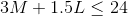

 orchestra answered 3 years ago
orchestra answered 3 years ago