Question

1) A neutron star is the collapsed remains of a massive star after it "dies". Use the law of conservation of angular momentum to explain why the neutron star spins faster than its parent star.

2) Consider lifting a 10-lb bag of flour (~50 N) 3 feet high (~1 m). To equal the power of a 100-W lightbulb, how fast must you lift the flour?

please answer in full, detail sentences

Answer 1

1. A neutron star is the collapsed remains of a massive star after it "dies". Use the law of conservation of angular momentum to explain why the neutron star spins faster than its parent star.

When the star dies and collapses into a neutron star, it retains its angular momentum.

Now Angular Momentum is L = m v r

Let the angular momentum before collapse : L₁ = m₁ v₁ r₁

Normally r₁ is about 10⁶ km. When it collapses into neutron star the radius shrinks by a huge amount, Usually size of a neutron star is about 10 - 100 km. So it shrinks by a factor of about 1000 at least.

Angular momentum after collapse: L₂ = m₂ v₂ r₂

Now mass before and after collapse doesnt change much. m₁ is approx. = m₂

r₁ = 1000 r₁

To keep the same angular momentum, v₂ (spinning speed) must therefore increase by large amounts.

So, for L₁ = L₂

m₁v₁r₁ = m₂v₂r₂

if m₁ = m_2`, r₁=1000 r₂ , then v₂ = m₁v₁r₁ /m₂r₂ or, m₁v₁r₁ 1000 /m₁r₁

or,

v₂ = 1000 v₁ Therefore when a star collapses into a neutron star, it spins much faster than its parent star to conserve its angular momentum.

2.

Consider lifting a 10-lb bag of flour (~50 N) 3 feet high (~1 m). To equal the power of a 100-W lightbulb, how fast must you lift the flour?

Power P = Work/time = Force * speed cos theta = F v cos (theta)

Here Force is force we apply against gravity (which is equal and opposite to gravitational force). Lift is also in same direction, so theta = 0deg or, cos(theta) =1

P = F v

Now v = distance /time = h/t

h= 3 feet = 0.9144 m

F = mg =10 lb * 9.8 m/s² = 4.54 kg * 9.8 m/s² =44.5 N

So for P = 100 W

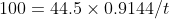
or, t = 2.46 seconds So we must lift the flour in this time to equal power of a 100 W light bulb.

And the speed of lift: v = 100/44.5 = 2.26 m/s