Question

Regents of a large state university proposed a plan to increase student fees in order to build new parking facilities. A news channel claims that over 70% of the students are opposed to the plan. We wish to test this claim. A random sample of 18 students is taken and 17 of them are opposed to the plan.

A- state the null and alternative hypothesis?

B- estimate the population proportions of students that are opposed to the plan?

C- finding the corresponding standard error for the estimate in part to B and use this standard error to provide an interval estimate for the population proportion with 95% confidence?

D-Calculate the test stastic and provide the p-value for testing the hypothesis. show all work?

E- give a one sentence conclusion in the contexet of this problem?

Answer 1

Claim: A news channel claim that over 70% of the students are opposed to the plan to increases student fees that is p > 0.70

A. Null and alternative hypothesis:

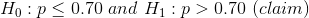
B. Estimate of the population proportion.

Sample proportion is the best point estimate of the population proportion.

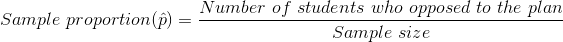
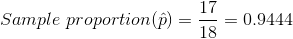
C. Interval estimate for the population proportion with 95% confidence.

The standard error of estimate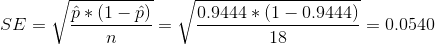

The formula of interval estimate for the population proportion is,

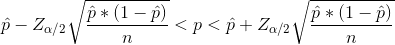
Where Z is the critical value at a given confidence level.

c = 95% = 0.95

alpha = 1 - c = 0.05

alpha/2 = 0.05/2 = 0.025

1 - (alpha/2) = 1 - 0.025 = 0.975

By using standard normal table the Z critical value for the area 0.9750 is 1.96

Plug all the values in the formula of interval estimate that is confidence interval,

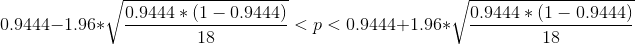
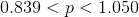
Proportion always lies between 0 to 1 both inclusive,

Therefore the inteval estimate for population proportion is (0.839, 1.000)

D. Test statistics and P-value.

The formula of z test statistics is,

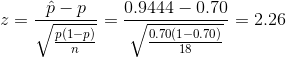
The test is a right-tailed test since the alternative hypothesis contains greater than sign.

P-value = P(Z > test statistics) = P(Z > 2.26)

By using standard normal table the probability for z = 2.26 is 0.9881, which is less than probability but we need greater than probability.

So P(Z > 2.26) = 1 - 0.9881 = 0.0119

P-value = 0.0119

Alpha = 0.025, according to the 95% confidence level

The confidence interval is two sided and here the testing is one sides, therefore that divides into half.

Decision: Here P-value < alpha so reject the null hypothesis that is in favor of an alternative that is claim.

E. Conclusion

Conclusion: Reject the null hypothesis that is there is sufficient evidence to support the claim that over 70% of the students opposed to the plan to increase student fees.